
今日はちょっといつもと違う雰囲気の記事です。検索で来られる方もおられるようなので、大学受験生向け(もしかしたら高校の先生向けにもなるかも)に「コンデンサーの極板間引力の求め方」というテーマで記事を書いてみたいと思います。
全部まとめたpdfを末尾に置いています。こちらの本文はそのダイジェスト版となります。
要約
コンデンサーの極板間引力Fを求める方法は、だいたい次の2つの方法のどちらかを使うことになっていると思います。
(1)片方の極板が受ける力(これがF)は、
自らの電荷Qと、相手が作る電場E/2の積だから
F = QE/2
である!
(2)コンデンサーに電荷Qを蓄えた状態で電池から切り離し、
Fに等しい外力を加えて極板間隔をΔdだけ広げたとすると・・・
加えた仕事がコンデンサーの静電エネルギーの増加量に等しいはずなので
FΔd = ΔU
が成り立つ。これを変形していくと同じ結果が得られる!
今回は、これらとは異なる方法でこの問題に取り組みました。
今回取り組んだこと
そもそも極板間引力とは、要するに
「極板にたまっている電気のプラスとマイナスどうしが引っぱり合う力」
のはずだから、点電荷が受ける力の公式(クーロンの法則)
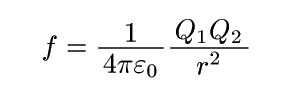
を利用しても導けるのではないか?・・・という、ありそうな疑問にそのまま取り組んでみました。
解く!
上の極板に+Q、下の極板に-Qの電荷がたまっているとします。
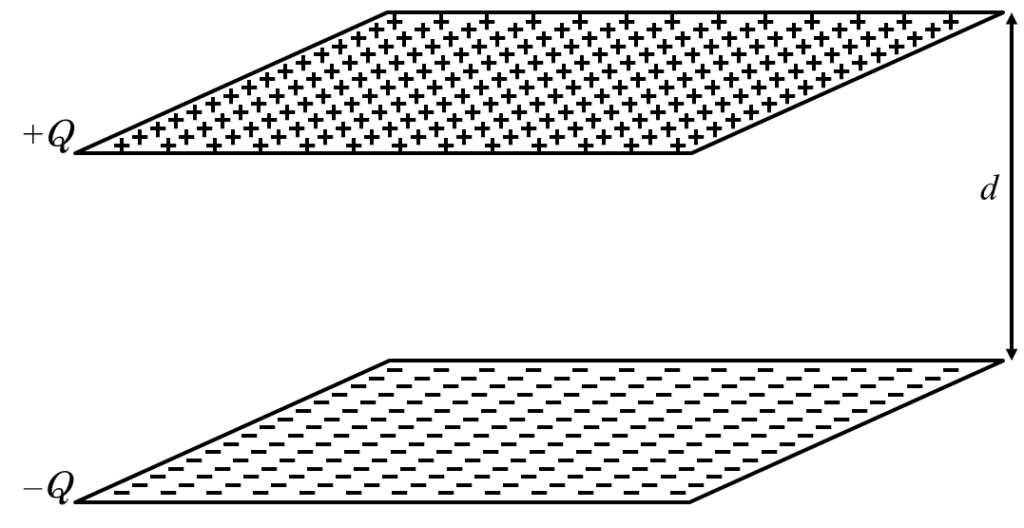
上の極板における小さな領域にある電荷qが下の極板の一部の電荷-q‘から受ける力f1を求め・・・
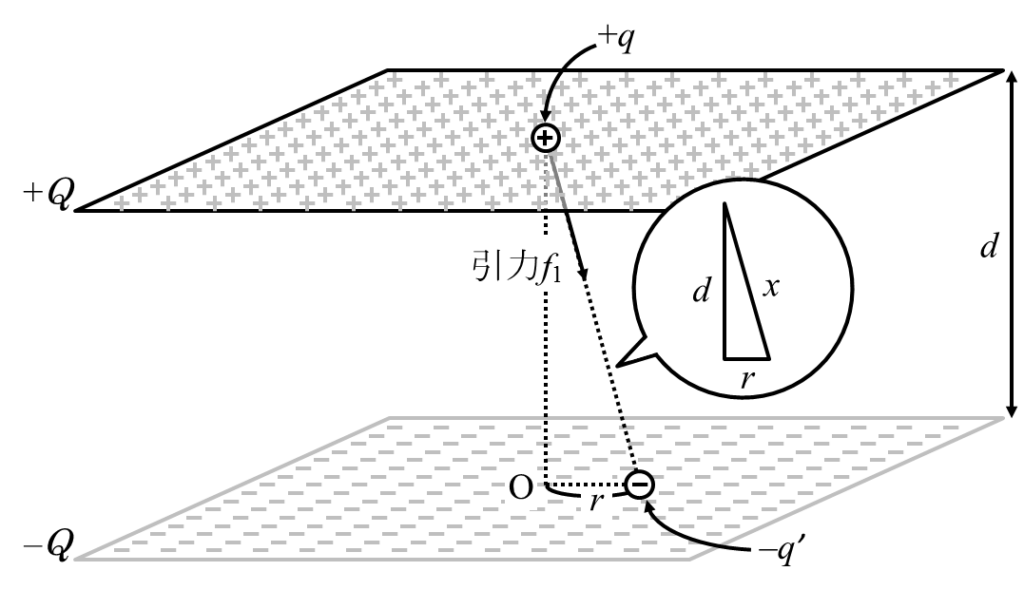
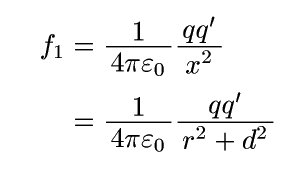
f1を全ての負電荷について足していけばいいのですが、その際は「垂直成分」f1cosθだけを足せばいいと分かるので・・・

こんな風にリング状の領域を想像していくと・・・
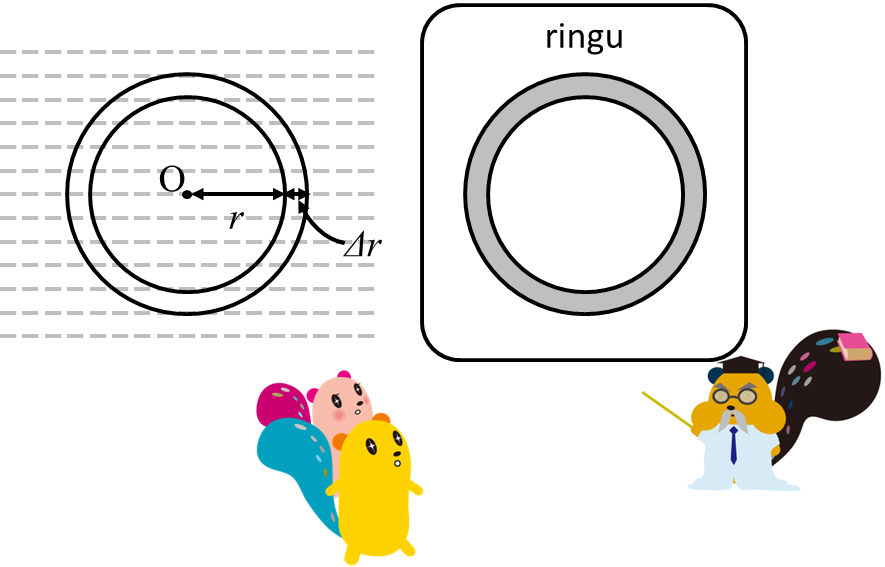
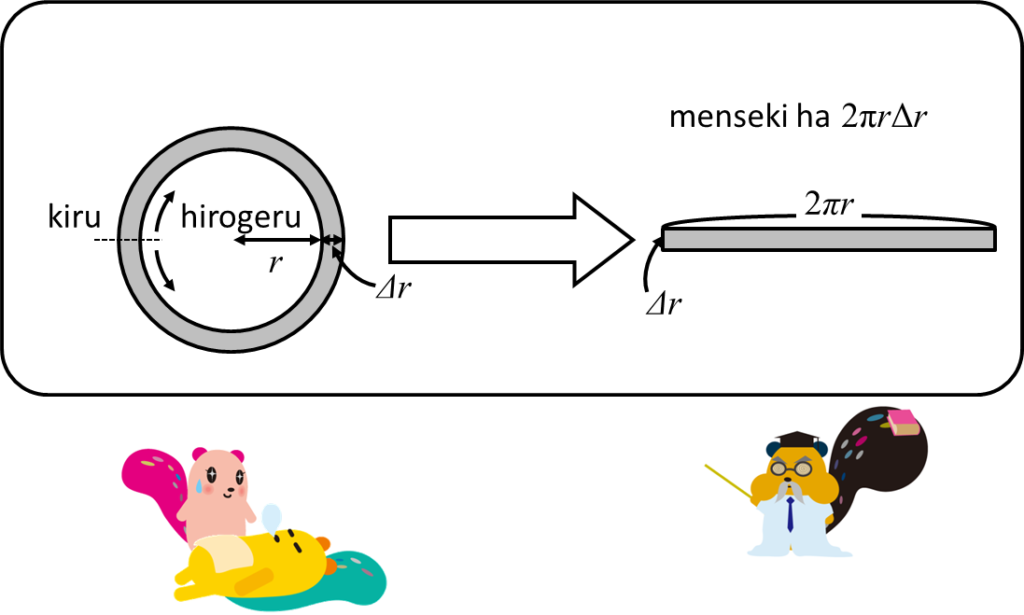
qが受ける力の合計ΔF1は次のように求められました。

あとはこれを全てのリングについて合計すればいいですね。これは積分という操作になりますね。小さなものを足し合わせる際に定積分を使えばよい、ということは数学IIIか何かで習うはずですので、まだ習っていない人には少しツライところですね。
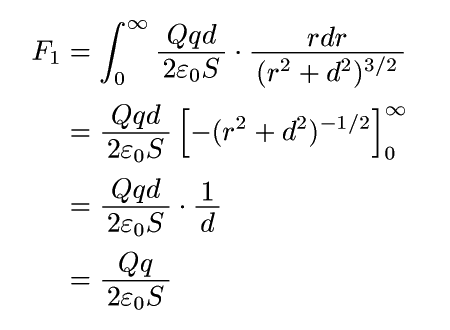
これがqが受ける力F1です。あとはqの方も全ての正電荷について合計すればいいので、qのところがQになって
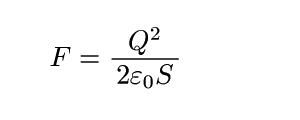
となり、目的達成です(このあとE=…という公式を使って書き直すと、F=QE/2になります)。
pdfはこちら
もうちょっと丁寧に書いたpdfをここに置いておきます。
こんなことを考えたわけ
前置きとして「ありそうな疑問に答えた」と述べましたが、まあお察しの通り、実際に大学受験生から寄せられた質問です。いわゆる「普通の求め方」はそれはそれで理解できるが、点電荷の集まりのはずなのにそれを使わない(または使えない?)のはなぜか?という。
大学入試が近くなってくると、数学の力もそれなりにこなれてくるので「こういうときは定積分を使えるね」「小さなリングは、切り開くとだいたい長方形ですね」ということが何となく分かってくるものですよね。こうやって理解できることは(時間の許す範囲で)探求していくと楽しいんじゃないでしょうか。
受験勉強が長くなると「今やっていることは、大学入試で効率的に点数を取るための手段だ」と考えがちだと思いますが、そうではなくて「実際に成り立っていることを色々な切り口で理解しようとしているプロセスなんだ」ということを少しでも感じてほしいんですよね。特に電気分野は目で見て感じることが難しいので、頭の中にあるいろいろな理論を組み合わせて理解を深めるといいと思います。
ほかのブログへ
↑クリックするといろんな科学ブログを探せます。ついでに「カガクのじかん」のランキングも上昇します(ありがとうございます)。







