
あることについて考えようとしていたときに、そこから派生してふと思ったことがあるんです。
例えば4桁の数abcdがあるとして、
abcd
_bcd
__cd
___d
の4つともが素数になるような数って、どのくらい珍しいんだろう?と(アンダーバーは左側に空白を入れるためのものです)。
素数度という呼び名
ここで唐突ですが「素数度」という呼び名を導入します。これは「与えられた数を上の桁から1つずつカットしていったとき、素数が何個得られるか」によって決めます。例をいくつか。
例1:123
123は素数でない(123=3×41)
_23は素数
__3は素数
よって123の素数度は2
例2:1239
1239は素数でない(1239=3x7x59)
_239は素数
__39は素数でない(39=3×13)
___9は素数でない(9=3×3)
よって1239の素数度は1
すると、気になるのは?
このように「素数度」を定めますと、当然気になるのは「素数度がNのN桁整数」ですよね?左から1つずつ数をカットしていくと全てが素数になるような。
例えば「113」は「素数度3の3桁整数」です。
113は素数
_13は素数
__3は素数
このような数はどのくらいあるんでしょうか?
と思って調べていると、こういう数のことを「左切り捨て可能素数 (left-truncatable prime)」と呼ぶのだと知りました(確かに左を切り捨てても素数になる数、という雰囲気のネーミングですね)ので、以下ではこの呼び名に統一します。ただ、以下で「N桁の左切り捨て可能素数」としばしば言わなければならない部分がありまして、それだと長すぎますので
「N桁の左切り捨て可能素数」→「N-左切素数」
と短縮して呼ぶことにします。させつそすう、と呼ぶと読みやすいと思います。
探索ルーチン
探索のアルゴリズム自体は難しくありません。
(1)まず1-左切素数(要するに1桁の素数)からスタートします。
2, 3, 5, 7 の4つですね。
(2)これらの数値の左に1~9を1つずつ付け加えて、それらが素数になるかどうかを調べます。
12, 22, 32, … , 92 → いずれも素数でない
13, 23, 33, … , 93 → この中の素数は13, 23, 43, 53, 74, 83
15, 25, 35, … , 95 → いずれも素数でない
17, 27, 37, … , 97 → この中の素数は17, 37, 47, 67, 97
そうすると、得られた「13, 23, 43, 53, 74, 83, 17, 37, 47, 67, 97」が「2-左切素数」ということになります。
(3)同じことを繰り返していけばいくらでも大きな桁のN-左切素数を探索できます。
ですのでエクセルのVBAを使って探索を始めました・・・のですが、エクセルって遅いんですよね。いつもこういう自由研究(笑)にはエクセルを使ってしまうのですが、どうにも遅いんです。8桁ぐらいまでは数秒で済むのですが、9桁以降は1桁調べるたびに10分とか20分かかるようになり、12桁以降は何時間というレベルに。18桁目に至ってはほぼ丸1日探索しても終わらない始末です。
というような途中経過の報告をFacebookで行ったところ、日頃お世話になっている某数学の先生が「PARI/GPという言語を使うと1秒ぐらいで済んだ」と教えてくださったのです。
1秒?なんかすごいプログラミングなのか?と思ったのですが、私もPARI/GPをインストールして試行錯誤でプログラムを組むと、なんとあっさり計算が終わってしまったのです!こんな出力が得られました。プログラムの力ではなくて言語の力なんですね・・・どうなってるんだか・・・。
PARI/GPのインストールなどについてはこちらの富山大学のページを参考にしましたが、要するに本家からインストーラをダウンロードして実行するだけでした。
めぼしい結果のまとめ
左切り捨て可能素数の全個数は4260個でした。多すぎますので別ファイル(テキスト)にしました。興味のある方はここ → left-truncatable_prime_all からダウンロードしてください。
桁ごとの個数はこんな感じです。
| 桁 | 個数 |
| 1 | 4 |
| 2 | 11 |
| 3 | 39 |
| 4 | 99 |
| 5 | 192 |
| 6 | 326 |
| 7 | 429 |
| 8 | 521 |
| 9 | 545 |
| 10 | 517 |
| 11 | 448 |
| 12 | 354 |
| 13 | 276 |
| 14 | 212 |
| 15 | 117 |
| 16 | 72 |
| 17 | 42 |
| 18 | 24 |
| 19 | 13 |
| 20 | 6 |
| 21 | 5 |
| 22 | 4 |
| 23 | 3 |
| 24 | 1 |
| 25 | 0 |
まあ、私が調べるまでもなくwikipediaとかに載っていましたが・・・。
なんと最大値がある!
ところで上の画面にも現れていますが、左切り捨て可能素数には最大値があります!まぁ新発見ではないので、ビックリマークをつけるほどのことではありませんが・・・。それでも、自分で興味を持って調べてみて結論まで得られたというのは嬉しいことです。
最大値は24桁の数で、
357686312646216567629137
です!つまり
357686312646216567629137
_57686312646216567629137
__7686312646216567629137
___686312646216567629137
____86312646216567629137
_____6312646216567629137
______312646216567629137
_______12646216567629137
________2646216567629137
_________646216567629137
__________46216567629137
___________6216567629137
____________216567629137
_____________16567629137
______________6567629137
_______________567629137
________________67629137
_________________7629137
__________________629137
___________________29137
____________________9137
_____________________137
______________________37
_______________________7
はすべて素数!!!ということです。
覚えにくいので語呂合わせで覚えましょう。ハイ!声を揃えて~!
3576863 1264 621656 7629137
「巫女南無野郎さ いじろうよ ムニ色五浪 なろ憎い皆」
そして残念ながら357686312646216567629137の左に1~9を追加してもどれも素数にならないのです。
1357686312646216567629137 = 229 x 21113957237 x 280798200169
2357686312646216567629137 = 3 x 37 x 21240417231046996104767
3357686312646216567629137 = 7 x 2039 x 235247412081988129169
4357686312646216567629137 = 911 x 542262449 x 8821207871183
5357686312646216567629137 = 3^2 x 1811 x 581390617 x 565390236139
6357686312646216567629137 = 11^2 x 61 x 1619 x 2347 x 26083 x 8690933183
7357686312646216567629137 = 23 x 353897 x 903933644245816127
8357686312646216567629137 = 3 x 328705131947 x 8475363378257
9357686312646216567629137 = 47 x 101 x 251 x 24953 x 314740596040657
(ちなみにこういう素因数分解もPARI/GPですぐできます。factor(1357686312646216567629137)などと入力すれば瞬時に答えが出ますよ)
最大値があるのは当たり前なのか?
このように「調べてみると最大値がありました」というのは、ぐうの音も出ない事実なわけですが、これって当たり前のことなんでしょうか、それとも何か珍しい事態を表しているのでしょうか。
珍しさを表す一つの指標として「各桁の素数の割合」と比較してみてはどうかな?と思いました。
例えば2桁の数は10~99の90個ありますが、素数は21個です(11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97)。素数の割合としては21/90=23%ですかね?ただ、この計算だと分母に2桁の数全てが入っていますが、今回の探索はそもそも3と7の2つの素数から始まったと言っても過言ではないですよね。2と5は2桁目に入った瞬間に消滅するのが明らか(10の位を追加する前から明らか)だからです。
なので分母に入るべき数は、「2桁の数全て=90個」ではなく、「2の倍数と5の倍数以外」ということになるんじゃないでしょうか。
2の倍数と5の倍数を除くということは、1の位が1,3,7,9の数だけをカウントすればいいので、2桁ならば「36個」となります。3桁ならば360個、4桁ならば3600個・・・のようになります。この数値を分母にして「素数の割合」を出してみると、2桁の場合は21/36=58%となります。結構ありますね。
ここまでの事情を表にしてみます。素数の個数はwikipediaの「素数計数関数」という項目を参照しました。
| 桁 | 数の個数(2と5の倍数を除く) | 素数の個数 | 素数割合 |
| 2 | 36 | 21 | 58% |
| 3 | 360 | 143 | 40% |
| 4 | 3.6×10^3 | 1061 | 29% |
| 5 | 3.6×10^4 | 8.36×10^3 | 23% |
| 6 | 3.6×10^5 | 6.89×10^4 | 19% |
| 7 | 3.6×10^6 | 5.86×10^5 | 16% |
| 8 | 3.6×10^7 | 5.10×10^6 | 14% |
| 9 | 3.6×10^8 | 4.51×10^7 | 13% |
| 10 | 3.6×10^9 | 4.04×10^8 | 11% |
| 11 | 3.6×10^10 | 3.66×10^9 | 10% |
| 12 | 3.6×10^11 | 3.35×10^10 | 9.3% |
| 13 | 3.6×10^12 | 3.08×10^11 | 8.6% |
| 14 | 3.6×10^13 | 2.86×10^12 | 7.9% |
| 15 | 3.6×10^14 | 2.66×10^13 | 7.4% |
| 16 | 3.6×10^15 | 2.49×10^14 | 6.9% |
| 17 | 3.6×10^16 | 2.34×10^15 | 6.5% |
| 18 | 3.6×10^17 | 2.21×10^16 | 6.1% |
| 19 | 3.6×10^18 | 2.09×10^17 | 5.8% |
| 20 | 3.6×10^19 | 1.99×10^18 | 5.5% |
| 21 | 3.6×10^20 | 1.89×10^19 | 5.3% |
| 22 | 3.6×10^21 | 1.80×10^20 | 5.0% |
| 23 | 3.6×10^22 | 1.72×10^21 | 4.8% |
| 24 | 3.6×10^23 | 1.65×10^22 | 4.6% |
| 25 | 3.6×10^24 | 1.58×10^23 | 4.4% |
| 26 | 3.6×10^25 | 1.52×10^24 | 4.2% |
桁が上がるにつれて素数の割合が徐々に減っていくんですね。ということは、
N-左切素数 → (N+1)-左切素数
と生成していく際に、(N+1)-左切素数の候補数はN-左切素数の9倍できますが、そのうち数%しか素数にならない・・・と考えると、徐々に左切素数の個数は減っていくんじゃないでしょうかね?
例えば21-左切素数から22-左切素数を作ることを考えます。21-左切素数の例として「367986315421273233617」を挙げますと、22-左切素数の候補は以下の9個あります。
1367986315421273233617
2367986315421273233617
3367986315421273233617
4367986315421273233617
5367986315421273233617
6367986315421273233617
7367986315421273233617
8367986315421273233617
9367986315421273233617
ですが、22桁の数における素数の割合は5.0%しかないわけです。9個のうちの5.0%は0.45個。ですからこの中に素数があるかないか、感覚的には五分五分ぐらいなのでは?と見積もることができます。
こんな風に1つのN-左切素数から9個の(N+1)-左切素数候補を作ったとき、候補の中にある素数の期待値が1を下回るのは、だいたい素数の割合が11%を切るあたりからだと思われます(9×0.11=0.99なので)。ということは、11桁目ぐらいから左切素数の個数は減っていくのでは?などと皮算用することができます。
表とグラフで「期待個数」と実際の個数を比較
ここまでの状況を表に表してみると次のようになります。
| 桁 | 実際の個数 | 期待個数 |
| 2 | 11 | 10.5 |
| 3 | 39 | 39.3 |
| 4 | 99 | 103.4 |
| 5 | 192 | 207.0 |
| 6 | 326 | 330.7 |
| 7 | 429 | 477.7 |
| 8 | 521 | 546.6 |
| 9 | 545 | 587.2 |
| 10 | 517 | 550.7 |
| 11 | 448 | 473.4 |
| 12 | 354 | 375.1 |
| 13 | 276 | 273.0 |
| 14 | 212 | 197.3 |
| 15 | 117 | 141.2 |
| 16 | 72 | 72.9 |
| 17 | 42 | 42.2 |
| 18 | 24 | 23.2 |
| 19 | 13 | 12.6 |
| 20 | 6 | 6.5 |
| 21 | 5 | 2.8 |
| 22 | 4 | 2.3 |
| 23 | 3 | 1.7 |
| 24 | 1 | 1.2 |
| 25 | 0 | 0.4 |
ここで「N桁の期待個数」の定義は次のようにしています。
N桁の期待個数 = (N-1)-左切素数の個数 x 9 x N桁の素数割合
例えばN=3に対してはこんな計算をしています。
3桁の期待個数 = 2-左切素数の個数 x 9 x 3桁の素数割合
= 11 x 9 x 0.397(表中では0.40)
= 39.303
なお、2桁の期待個数を出す際には1-左切素数の個数を用いる必要がありますが、
1-左切素数の個数 = 2個(3と7のみ / 2と5は除外)
としています。これは「2と5の左にどんな数をくっつけても絶対素数にならない」ということが数をくっつける前から明らかだから、除いた方がいいんじゃないかなと思ってのことです。
グラフで表現するとこうなります。普通のグラフと、縦軸を対数表示にしたものを掲載します。
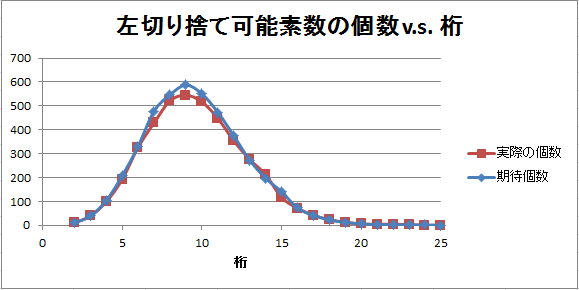
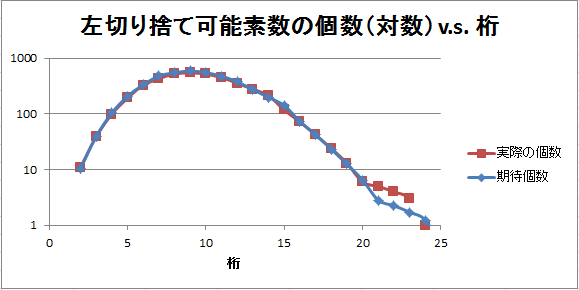
・・・どうでしょう?ものすごい一致!と言ってもいいですし、細かく見ると「10桁前後では期待個数がやや多く、20桁以降では実際の個数の方がやや多い」という傾向が見られますね・・・と言ってもいいですね。これが何かを意味しているのかどうかはよく分かりませんが・・・。
「理論期待個数」なんてものを考えることもできる
先ほど考えたのは、(N-1)-左切素数の個数からN桁の期待個数を算出するということでした。実際の個数から次の桁の期待個数を算出するという考えです。
これに対して、最初の左切素数の個数に「9x素数割合」をどんどんかけていっていくらでも大きな桁の期待素数を定めることもできます。これを「理論期待個数」と呼ぶことにしましょう。つまり例えばこんな感じです。
2桁の理論期待個数 = 1-左切素数の個数 x 9 x 2桁の素数割合
3桁の理論期待個数 = 2桁の理論期待個数 x 9 x 3桁の素数割合
4桁の理論期待個数 = 3桁の理論期待個数 x 9 x 4桁の素数割合
・・・
このように定めると、実際に1つ1つの数が素数かどうかを調べる前に「たぶんそれぞれの桁にこのぐらい左切素数が現れるだろうな」と見積もることができるんじゃないかな~と思います。
グラフで表すとこんな感じです。
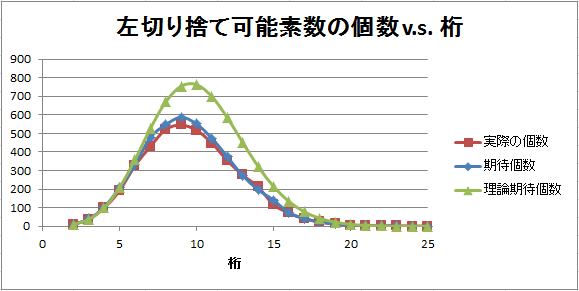
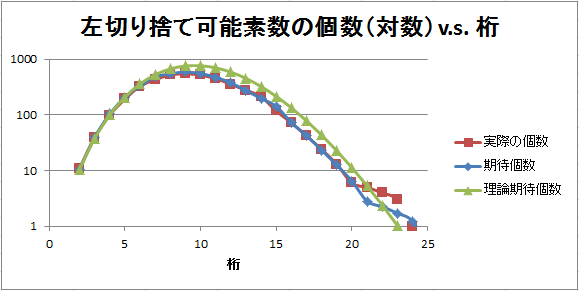
10桁前後ではだいぶ理論期待個数が実際を上回っていますが、面白いことに24桁まで来ると理論期待個数は0.42個となっています。実際には24桁には1個だけあったわけですが、そのことが最初から予言できる、とも言えますね。予言は言い過ぎかな、「見積もりができた」という感じでしょうか。
まとめ
- ふとした興味から「左切り捨て可能素数」について調べた。
- 私が調べるまでもなく知られている事実だったけども、一応全リストや桁ごとの個数を掲載。
- 最大の左切り捨て可能素数は24桁の「357686312646216567629137」で、語呂合わせとして「巫女南無野郎さ いじろうよ ムニ色五浪 なろ憎い皆」を提案。
- そもそも左切り捨て可能素数は、桁を増やすごとに現在の9倍しか候補数が作られないため、新しい桁での素数割合が11%を切るあたりから減少することが予想される。実際そのようになっていて、期待値が1を切るのがちょうど25桁であった。実際の個数分布はこのような見積もりに大体合っている。
- ただし細かく見ると、期待個数と実際の個数がやや大きくズレているように見える箇所もあり(10桁前後と20桁以上)、これが何か大きな意味があるのかないのかは不明。
- PARI/GPは非常に強力!素数とかをチョチョッと調べてみるのに好適!!
いや~、何でも調べてみると面白いですね。






