
前の記事では、左から1つずつ数字をカットしても全部素数になるような数「左切り捨て可能素数」について調べました。例えば「9137」ですね。9137も素数、137も素数、37も素数、7も素数です。まだお読みでない方はコチラを先にどうぞ!
今回の記事ではこれと同じようなことを「年月日」に対して考えてみたいと思います。
「20191231」みたいな年月日
今回考えたいのは例えば「20191231」みたいな年月日です。この日付は
20191231 = 素数
191231 = 素数
1231 = 素数
31 = 素数
という代物です。こういう日付ってどのくらいあるんだろう?と興味を持ったのです。「左切り捨て可能素数年月日」とでも呼びましょうか・・・ちょっと長すぎるので「どう切っても素数の年月日」・・・これも長いですね。素数が4つ含まれているという意味をこめて「4素数年月日」はどうですかね。とりあえず以下ではそう呼ぶことにしましょう。
数え上げる方法
まぁ1000年1月1日(10000101)から1日ずつ増やしていって調べてもいいのですが(私は当初そのようにしたのですが)、今思えば「左切り捨て可能素数」と同様に、右側から順番に構築していった方が良かったですね。つまり以下のような手順です。
素数の「日」
いま考えようとしている年月日をYYyymmddと表すことにします。
YYyymmdd = 素数
yymmdd = 素数
mmdd = 素数
dd = 素数
となるわけですから、一番考えやすいのは「dd = 素数」の部分です。これは手作業でピックアップできますね。03 07 11 13 17 19 23 29 31 の9日だけです。
「月日」も「日」も素数なのは
次に考えるのは、「mmddもddも両方素数」になるようなmmddです。ddが素数なのは先ほどピックアップした9日ですから、これに01~12のmmをくっつけて、素数かどうか調べればよいですね。
調査する数字の個数は12×9=108個ですから、手作業でもできそうではありますが、そろそろ面倒になってきたのでエクセルを使いました。
以下が「mmddもddも両方素数になる月日」です。39個あるようですね。
0103 0107 0113 0131
0211 0223 0229
0307 0311 0313 0317 0331
0419
0503 0523
0607 0613 0617 0619
0719
0811 0823 0829
0907 0911 0919 0929
1013 1019 1031
1103 1117 1123 1129
1213 1217 1223 1229 1231
念のためですが、例えば「0103」なんてのは最初のゼロは無視して103と3が素数である、という意味です。
西暦下2桁+月日(yymmdd)ではどうか
次に考えるのは、西暦下2桁だけを用いた「yymmdd」という形式の日付です。yymmdd, mmdd, ddの3つともが素数になるようなyymmddはどのくらいあるでしょうか。先ほど見つけた39個の日付に01~99の99個のyyをくっつけて調べればOKです。39×99=3861個の数を調査することになりますので、いくら何でも手作業はつらいですね。エクセルに頼ります。
数えてみると794個あるようでした。全部本文中に書くと大変なので、別ファイルにしました。こちらからどうぞ。
一番早いのは010103、一番遅いのは991229ですね。なお、yyとして00は入れていません。
いよいよ「4素数年月日」を調べる!
この794個の日付に10~99の90個のYYをくっつけて、それらが素数になるかどうかを調べればいいですね。ただし「うるう年」に関する配慮が必要です。
以下の2つのどちらかを満たす年がうるう年なんだそうです。
・400で割り切れる
・100で割り切れずかつ4で割り切ることができる
まぁ言い換えると「基本的には4で割り切れる年がうるう年だが、100で割り切れる年はうるう年から外す・・・と思いきや400で割り切れるならやっぱりうるう年」というルールですね。例えば「2000年」は100で割り切れますが400でも割り切れますのでうるう年です。
このルールを考慮して数え上げたつもりですが、うまくいったでしょうかね・・・9735個の「4素数年月日」が見つかりました。一番昔なのが10020107、最も未来なのが99990307です。全リストはこちらからどうぞ。
最近の「4素数年月日」
2019年には5つの「4素数年月日」が見つかりました。
20190523
20190613
20190811
20190823
20191231
です。大みそかが該当していますね。味わい深い年の瀬になりそうですね。
ところが2020年には1日もないのです。さかのぼれば2018年には2日ありましたが(20180311, 20181019)、2017年と2016年には1日もありません。ですからここ近年では、今年は異例に「4素数年月日」が多い年だと言えそうです。
「4素数年月日」はどのくらい珍しいのか
1000年から9999年までの各年に「4素数年月日」が何日ずつ含まれるかを数えてみました。1000年はもちろん0日ですが(yyが00のため)、1001年も0日。1002年に1日。このようなデータが得られました。
表にしてみるとこんな感じです。
| 日数 | 頻度 | 割合 |
| 0 | 3828 | 43% |
| 1 | 2343 | 26% |
| 2 | 1673 | 19% |
| 3 | 737 | 8.2% |
| 4 | 290 | 3.2% |
| 5 | 107 | 1.2% |
| 6 | 16 | 0.18% |
| 7 | 4 | 0.04% |
| 8 | 2 | 0.02% |
こうしてみると、2019年の「5日」というのはかなり異例に多い方ですね。5日以上を合算しても1.4%くらいしかありません(ちなみに21世紀中に5日以上の年は2019年しかなく、20世紀にも1956年の1回しかありません。22世紀には5回もありますが)。このような探究をしようと思い立ったのも、もしかすると素数のオーラ(?)が生活に充満しているためかもしれません。
それはさておきグラフにするとこんな感じです。普通のグラフと対数グラフです。
ウーム、何を読み取ればいいのかちょっと分かりませんね。
珍しさには周期性が!!
ところで上にチラッと書いたことを再度書いてみます。
「4素数年月日」を5日以上含む年は・・・
20世紀中に1回
21世紀中に1回
22世紀中に5回
このようにばらつきがある・・・ような・・・。サンプル数が少なすぎると意味のあることが言えそうにないので、「5日以上」と限ることなく、全部カウントしてみました。世紀ごとの「4素数年月日」の日数を数えてみると次のようになりました。全部載せるとまた大変なので16世紀から22世紀までです。
| 世紀 | 日数 |
| 16 | 168 |
| 17 | 89 |
| 18 | 77 |
| 19 | 164 |
| 20 | 94 |
| 21 | 82 |
| 22 | 182 |
ホラ、不気味な傾向が・・・?11世紀から100世紀までの日数を全部グラフにするとこうなります。グラフのタイトルをミスっておりますが「4素数年月日」の日数を数えております。
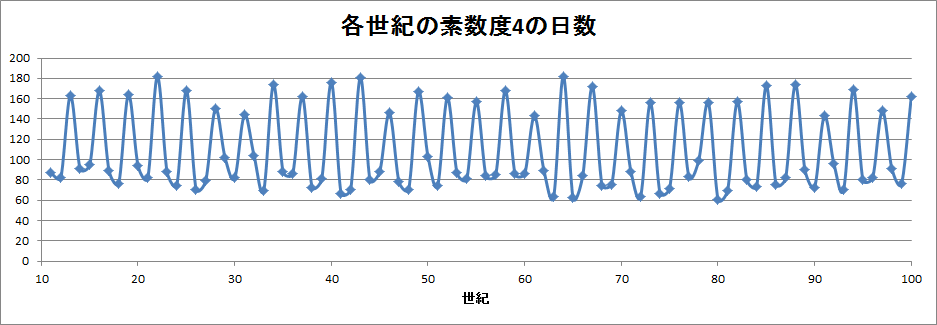
うおお!明らかですね。明確に3年周期が見えています。これは偶然でしょうか?しかし偶然かなと思うことにも大抵理由があるものです。考えてみましょう!
周期性の理由を考察
「4素数年月日」の日数に見られる明確な3世紀ごとの周期。その理由を考えてみるとわりとシンプルでした。3世紀ごとの繰り返しということは「3の倍数」と関係があるのでは?と思って以下のように考えました。ここで使うのは以下の性質です。
各位の数の合計が3の倍数なら、元の数は3の倍数
例:1+2+3=6が3の倍数なので、123は3の倍数。
例えば20世紀・21世紀・22世紀を比較することを考えます。yymmddの時点で「4素数年月日」の候補(yymmdd, mmdd, ddの3つともが素数であるような日付)が794個見つかっています。この794個のそれぞれに19, 20, 21をくっつけて、それらの数が素数になれば晴れて「4素数年月日」と認定される、というわけですが・・・。
例:191231に19,20,21をくっつけて
19191231→素数でない
20191231→素数!
21191231→素数でない
ここでそもそも「191231」の各位の数を足すと17ですから3の倍数+2です。ということは、この左にくっつけるYYが「3の倍数+1」であれば、「YY191231」はぴったり3の倍数となりますので、絶対素数になりません。上の例であればYY=19(3の倍数+1)をくっつけると「19191231」は3の倍数になりますから、素数かどうかを調べるまでもなく絶対に素数でないと分かるわけです。
一般的に書くとこういうことです。
yymmddが「3の倍数+2」であれば、YYが「3の倍数+1」のとき、YYyymmddは3の倍数になってしまう(絶対素数にならない)。
yymmddが「3の倍数+1」であれば、YYが「3の倍数+2」のとき、YYyymmddは3の倍数になってしまう(絶対素数にならない)。
yymmddが「3の倍数」になることはない(すでに除外されている)。
以上より、YYが「3の倍数」であれば、YYyymmddは3の倍数にはならないから、素数である可能性が出てくる。
ニュアンス伝わりますかね?表現を変えると以下のように言えます。
YYが「3の倍数+1」→yymmddが「3の倍数+2」であるケースを捨てている。
YYが「3の倍数+2」→yymmddが「3の倍数+1」であるケースを捨てている。
YYが「3の倍数」→全てのyymmddが「4素数年月日」の候補に残る。
ですから、yymmddを3で割った余りが2と1に半々に分布していて、かつ素数の出現確率にも偏りがないと仮定すると、YYが3の倍数である世紀は、ほかの世紀に比べて2倍程度の「4素数年月日」が登場するのではないかと見積もることができます。ちなみに22世紀はYY=21ですから「YYが3の倍数である世紀」ですね。
周期性の実際
yymmddを3で割った余りは数え上げることができまして、次のようになっています。
yymmddが「3の倍数+2」→386個
yymmddが「3の倍数+1」→408個
ほぼ半々ですね。
また、YYが3の倍数であるケースとその他のケースで「4素数年月日」の日数は次のようになっていました。
YYが3の倍数→4870日
YYがそれ以外→4865日
非常に拮抗していますね。上で考察したことはだいたい的を射ているのではないでしょうか。
「4素数年月日」の間隔
今年(2019年)は「4素数年月日」が割と多いのでありがたみが薄いのですが、先に述べたように来年(2020年)には1日もありません。ですので2019年の大みそかは存分に楽しまねばならない(何を?)わけですが、こうなってくると気になるのは「次の『4素数年月日』までの日数」はどのくらいが普通なのか、みたいなことです。調べてみました。
調べると言いましても、私の好きなエクセルは1900年より前の日付に対応していませんので、自分で日付間隔を算出するルーチンを作って計算しました。うるう年には対応させたつもりです。その結果がこちらです。
| 範囲 | 頻度 | 割合 |
| 99日以下 | 3060 | 31% |
| 100-199 | 1882 | 19% |
| 200-299 | 1215 | 12% |
| 300-399 | 775 | 8.0% |
| 400-499 | 558 | 5.7% |
| 500-599 | 462 | 4.7% |
| 600-699 | 368 | 3.8% |
| 700-799 | 312 | 3.2% |
| 800-899 | 241 | 2.5% |
| 900-999 | 225 | 2.3% |
| 1000-1099 | 188 | 1.9% |
| 1100-1199 | 118 | 1.2% |
| 1200-1299 | 77 | 0.79% |
| 1300-1399 | 45 | 0.46% |
| 1400-1499 | 22 | 0.23% |
| 1500-1599 | 35 | 0.36% |
| 1600-1699 | 23 | 0.24% |
| 1700-1799 | 18 | 0.18% |
| 1800-1899 | 24 | 0.25% |
| 1900-1999 | 14 | 0.14% |
| 2000-2099 | 20 | 0.21% |
| 2100-2199 | 11 | 0.11% |
| 2200-2299 | 7 | 0.07% |
| 2300-2399 | 9 | 0.09% |
| 2400-2499 | 5 | 0.05% |
| 2500-2599 | 4 | 0.04% |
| 2600-2699 | 2 | 0.02% |
| 2700-2799 | 2 | 0.02% |
| 2800-2899 | 1 | 0.01% |
| 2900-2999 | 3 | 0.03% |
| 3000-3099 | 2 | 0.02% |
| 3100-3199 | 2 | 0.02% |
| 3200-3299 | 0 | 0.00% |
| 3300-3399 | 1 | 0.01% |
| 3400-3499 | 2 | 0.02% |
| 3500-3599 | 0 | 0.00% |
| 3600-3699 | 0 | 0.00% |
| 3700-3799 | 0 | 0.00% |
| 3800-3899 | 0 | 0.00% |
| 3900-3999 | 0 | 0.00% |
| 4000-4099 | 1 | 0.01% |
100日以下というのが32%を占めていますし、「365日以下」にすると69%になります。ですから4素数年月日の7割は1年以内に再度訪れるわけですね(この表現で大丈夫なのか多少気になりますが)。
一方で2020年には1日もないのです。20191231の次は20210131ですので、間隔は397日です。このように1年を超える間隔のものもチラホラあり、一番長いのはなんと4040日です!
64750223
↓
↓この間が4040日!
↓
64860317
6475年という日付に少々気が遠くなりますが、とりあえず全貌をグラフで表してみるとこうなりました。縦軸は対数になっています。

このグラフから何かを感じ取るのは少々難しいのですが、まぁ結果として残しておきます。何かを発見した方はぜひ教えてください。
ちなみに一番短い間隔は「2日」です。これらの日々です。これを書いている日から遠い日付ばかりで現実感がありませんが・・・。
15510617, 15510619
21330311, 21330313
24571229, 24571231
27750311, 27750313
27871229, 27871231
30211229, 30211231
39750311, 39750313
45660617, 45660619
48330311, 48330313
51660617, 51660619
63571229, 63571231
63871229, 63871231
72930617, 72930619
81330311, 81330313
81750311, 81750313
他にも「1年」(365日or366日)というのも面白いですね。これだけあります。まぁやはり現在から遠すぎてイメージが湧きませんが・・・。
12830911, 12840911
12900103, 12910103
18450829, 18460829
21230719, 21240719
24120619, 24130619
24361213, 24371213
24420811, 24430811
24721117, 24731117
27980503, 27990503
33570919, 33580919
36440311, 36450311
45381103, 45391103
48600823, 48610823
48630919, 48640919
51031231, 51041231
54290317, 54300317
54561229, 54571229
54630613, 54640613
54771217, 54781217
54800419, 54810419
57440311, 57450311
60560113, 60570113
60630907, 60640907
66810223, 66820223
69600823, 69610823
72361213, 72371213
72570919, 72580919
75200131, 75210131
84450829, 84460829
90980503, 90990503
93561229, 93571229
96720619, 96730619
「4素数年月日」のできごと
wikipediaには例えば「1月3日」などという風に各日付の項目があります。こういうの誰が調べて書いているんですかね。その熱意に敬意を表します。
そこで「4素数年月日」に起こった事件がないか調べてみました。
結構見つかるかなと思ったのですが、案外少なかったですね。しかも結構悲しい事件(人命が失われるなど)も多かったので、ここに列挙するのはやめておきます。わりと無難だったのはこの日付ですね。
20070823
クリス・メッシーナがTwitterで「#」を記事のタグ付け記号にすることを提案。ハッシュタグの誕生。
ですから例えば今年の大晦日にこんなハッシュタグだらけの投稿をするのも乙なのではないでしょうか。
#20191231は素数 #191231も素数 #1231も素数 #31も素数 #の誕生日20070823も同じ
まとめとおまけ
- YYyymmdd, yymmdd, mmdd, ddの4つともが素数になるような年月日「4素数年月日」を調べた。
- 9735個の4素数年月日が見つかった。
- 4素数年月日の日数は3世紀ごとの周期があり、21世紀は少ない世紀である。
- 2019年には21世紀としては異例に多くの4素数年月日が含まれる(5日)。ちなみに大みそかも4素数年月日。
- 2020年には4素数年月日は1日もない。
- 近接する4素数年月日までの日数のうち最も長いのは、64750223から64860317までの「4040日」である。
このことを調べているとき、ちょうど東映のオフィシャルアカウントで「未来戦隊タイムレンジャー」という作品の再放送をしていたのを観ていました。この作品では30世紀から未来人4人が2000年にタイムスリップしてきます。4人はそこで出会った現代人の男、竜也とともにタイムレンジャーとなり、同じくタイムスリップしてきた犯罪者集団を逮捕していく・・・という設定です。
最終回では未来人達はもとの30世紀に帰っていき、1人残された竜也はこうつぶやきます。
「お前達は1000年先にいる。俺はそこへ向かってるんだ。たどり着くわけないけど。でも、お前達とは確実につながってる。俺がこれから作る明日(あした)っていう時間の中で」
そうなんです。竜也が未来人達と別れたのは2001年2月4日。そこから3000年までの間に1079日の4素数年月日があります。この途方もない日数を人類が無事通過して、ようやく3000年の未来にたどり着けるというわけです。書きながら少し不安になってきました。1000年先の未来はとても想像できませんが、1000年後はまぎれもなく「明日」の延長上にあるんだということを思いつつ暮らしていきたいものです。






