
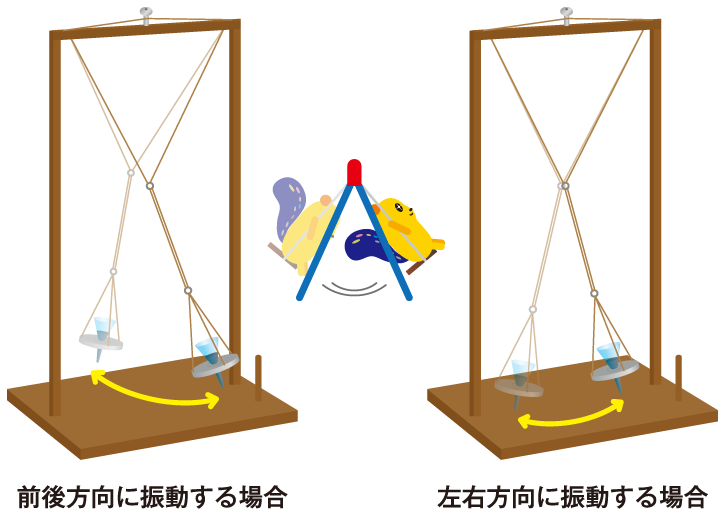
1本のひもにおもりがついたような「普通の振り子」を振ると、直線的な往復運動になりますよね。しかし、次の図のように「Yの字」の糸におもりをつけた振り子だと・・・?

ブラックバーンの振り子というそうです
このような形の振り子は「ブラックバーンの振り子 (Blackburn pendulum)」と呼ばれるそうです(と言っても、意外と振り子の写真と名称を一緒に記した資料が見つからないので次の3つをどうぞ→大阪市立科学館・けんさく。さんのブログ・芸術作品の紹介(英語))。
大まかに言うと、ブラックバーンの振り子はYの字に対して左右方向に振動するときは「短い振り子」のようになり、前後方向に振動するときは「長い振り子」のようになります。振り子の周期は主にひもの長さで決まりますので、ブラックバーン振り子は、縦方向と横方向で振動の周期が異なるということになります。
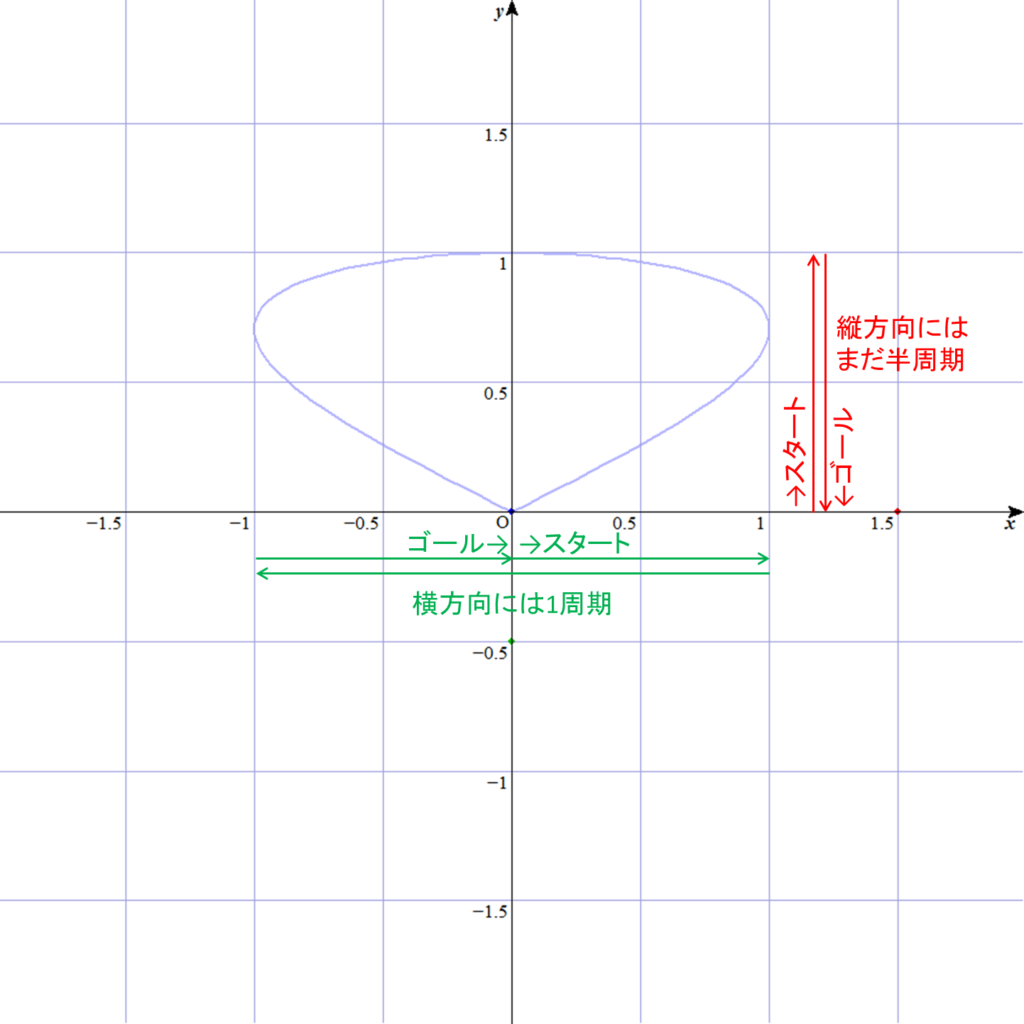
すると、「横方向に1周期振動しても、縦方向にはまだ1周期振動していない」みたいなことが起こりますので、振り子は平面上を複雑な図形を描きながら運動します。例えば、振り子が「横方向に1周期、縦方向に半周期」だけ動いた場合は次のような図形になります。緑の点が「横方向の振動」を表していて、赤い点が「縦方向の振動」を表します。両方が合成されたのが青い点で、これが実際の振り子の動きに相当します。GIFアニメはこちらです。

GIFアニメが再生できない方用の静止画像はこちらです。横方向には1周期動いて、縦方向に半周期だけ動くと、こんな感じになります。
ではいろんな条件で試してみると?
例えば縦方向の周期と横方向の周期を6と4に設定して(6秒と4秒みたいな意味です)みると、次のようになります。周期のほかに、「縦方向と横方向の位相のずれ」という値を決めることができます。この値を変えると振動のスタート地点が変わるのですが、その結果として、できる図形も変わってくるみたいです。
以下は、周期6秒と4秒で、位相のずれの値を4種類試してみたものです。
★周期6と4。位相のずれ0。
何となくプロレスラーやスーパー戦隊のマスクを思わせる輪郭を通過し、以後は同じ道を何度も辿っていきます。
★周期6と4。位相のずれ0.1π。
「α」の文字が左右反転したような輪郭を通過し、以後は同じ道を何度も辿っていきます。
★周期6と4。位相のずれ0.2π。
位相のずれ0のときに描けるスーパー戦隊のマスクみたいな輪郭を、ちょっと斜めから見たようなムードの図形ですね。途中からは同じ道を何度も辿っていきます。
★周期6と4。位相のずれ0.3π。
位相のずれ0.2を左右反転させたような図形ですね。途中からは同じ道を何度も辿っていきます。
きれいですね。こういう風に縦横に異なる周期をもつ振動が合わさってできる模様のことを「リサジュー図形」といいます(リサージュ図形ともいいます)。周期の組み合わせや初期位置によってさまざまな模様になります。いろいろな模様は例えばここで見ることができます。
必ず繰り返し図形になるか?
「6秒と4秒」のように、縦横の周期に公倍数がある場合は、「公倍数ぶん」だけ時間が経てばもとの状態に戻ることがすぐ想像できますよね。タテ6秒・ヨコ4秒の例なら、タテに2往復、ヨコに3往復すれば12秒経ちますから、もとの状態に戻ったことになります。だから以後の運動はこの12秒の運動の繰り返しとなります。
では、どんな周期の組み合わせでもこういう風にうまくいくのでしょうか?
どんな整数でも公倍数はあるから、うまくいくのでは?・・・と思った方は鋭いですね。そうですね、例えば3と7なら21、5と9なら45、のように、2つ適当な整数を取ってくれば必ず公倍数はあります。aとbならabが必ず公倍数になるというわけです(abが最小公倍数かどうかは分かりませんが)。ですので、2つの周期が整数なら、「何回か繰り返してもとに戻る」ということが必ず起こりますね。
しかし、いま考えている2つの周期は、必ずしも整数である必要はありません。例えば3.1秒とか、1.77秒とか、そういう小数でもいいわけです。あるいは1/3秒とか2/7秒のような分数でも構いませんよね。そういう場合でも公倍数ってあるのでしょうか?というか、「整数回の往復でもとの状態に戻ることができるか」ということを知りたいですよね。
でも、周期が小数や分数の場合は、「整数回の往復でもとの状態に戻ることができる」ことがすぐ想像できます。例えば・・・
例:周期がタテ1.2秒とヨコ0.7秒の場合
→両方の数値に10をかけて(10往復する時間です)12秒と7秒の公倍数、すなわち12×7=84秒という数字を求めます。これは「タテにちょうど70回、ヨコにちょうど120回」往復する時間です。
例:周期がタテ1/3秒とヨコ2/7秒の場合
→両方の数値に21をかけた時間(21往復する時間です)である7秒と6秒の公倍数、すなわち7×6=42秒という数字を求めます。これは「タテにちょうど126回、ヨコにちょうど147回」往復する時間です。
周期が「有理数」ならもとに戻れる
ここまで述べてきたのは、よく考えると「有限桁数で終わる小数(1.2や0.7)」や、「小数にすると無限に続くけども分数で表せる数(1/3や2/7)」ですよね。有限桁数で終わる小数は、結局は分数で表せるので(例:1.2 = 6/5など)、ここまでに例として挙げた数は結局すべて「分数で表せる数」であると言えます。
こういう数はまとめて「有理数」といいます。普通は次のように定義します。高1ぐらいの数学で習うんでしたっけ。
有理数 = 整数/整数 で表せる数
ちなみに整数以外の有理数を小数で表示すると、有限桁数で終わるか、または循環小数になります。例えばこんな感じです。
- 1/2 = 0.5(有限桁数で終わる)
- 1/3 = 0.3333….(3が無限に続く循環小数)
- 1/4 = 0.25(有限桁数で終わる)
- 1/5 = 0.2(有限桁数で終わる)
- 1/6 = 0.1666…(1のあと6が無限に続く循環小数)
- 1/7 = 0.142857142….(142857が無限に続く循環小数)
2つの周期がともに有理数で、a/bとp/qという風に表されているとすれば、とりあえず周期をbq倍すればaqとpbという整数になりますから、その公倍数を求めれば必ず「整数回の往復でもとに戻る」と言えますね。一安心です。
整数回の往復でもとに戻れない場合は?~無理数の登場~
しかし、世の中には「分数でうまく表せない数」も存在します。それが「無理数」と呼ばれる数です。例えば√2とかπ(円周率)などが有名です。
無理数=整数/整数で表せない数
- √2=1.41421356….(ひとよひとよにひとみごろ【一夜一夜に人見頃】・・・)
- π=3.14159265….(さんいしいこくにむこぅ【産医師異国に向こう】・・・)
振り子の2つの周期の比率がもし無理数比だったらどうでしょうか?例えば縦の周期がa秒で、横の周期がaの√2倍だったら、整数回の往復でもとに戻れるでしょうか?
a×N = a×√2×M
となるような整数NとMがあるか?ということですが、もしそんなのがあったら
N = √2×M
となってしまいまして、結局
N/M = √2
となるので、「√2は分数で表せない数、つまり無理数である」ということに反してしまいますよね。なのでこのような整数NとMは存在しないわけです(こういう思考回路を「背理法」といいますね)。
したがって、縦横の周期の比率が無理数比だったら、振り子はもとの状態に戻ってくることができません!
元に戻れない振り子の軌跡
そういう、元に戻れない周期の組み合わせでリサジュー図形を描いてみました。縦横の周期を「6秒」と「√13秒」にしてみて、位相のずれを3種類試してみました。位相のずれをちょっと変えるだけで、ずいぶん個性的な図形が描けるのだなあと思います。
★周期6と√13。位相のずれ0
これは一貫してじわじわと行動範囲を広げていくような感じですね。
★周期6と√13。位相のずれ0.2π
これははじめにある程度の移動範囲を確保して、その中をまず埋めていく。埋まったら少しずつ移動範囲の端へと点が移動していき、少しずつ移動範囲を広げていく・・・というイメージですね。
★周期6と√13。位相のずれ0.3π
これは初期段階でいくつかの移動範囲を確定させて、その細い道を少しずつ全部膨らませていく感じです。
まとめ
今回の記事は大変長くなりましたが、まとめるとこんな感じの記事でした。
(1) リサジュー図形というものがある。これは振り子を縦横に異なる周期で振らせるとできる図形である。縦横の周期と「位相のずれ」というパラメータで図形の形が変わる。
(2) 縦横の周期が有理数の場合(記事中には十分表現していませんが、実際には縦横の周期そのものは有理数である必要はなく、「周期の比率」が「有理数比」だったらOKです)は、振り子は何回か往復すれば元の軌跡に戻ってくる。
(3) 縦横の周期の比率が無理数比の場合は、何回往復しても元の軌跡に戻ることはできない。「位相のずれ」をちょっと変えるだけで、ずいぶん個性的な図形が描ける。
ほかのブログへ
↑クリックするといろんな科学ブログを探せます。ついでに「カガクのじかん」のランキングも上昇します(ありがとうございます)。






