
プッカというお菓子があります。
一口サイズのプレッツェルの中にチョコレートが入ったもので、カリカリポリポリと結構いくらでも食べられてしまいます。プレッツェルの形はいろいろな魚や貝を模したものになっています。1箱43g入りだそうですが、個数を数えてみると19個入っていました。
ある日、プッカを2人で食べようと思って何気なく分けてみましたところ・・・
な、なんと!こんな風に分かれてしまいました。

怪奇現象!
お分かりいただけますでしょうか?先ほどの写真は、左の皿には1種類しか入っていません。右の皿には全種類のプッカが入っています。
実際の作業としては、箱の中から2個ずつつまんで皿に取っていきました。2個つまんで左の皿へ。2個つまんで右の皿へ。これを繰り返していました。途中で「あれっ?こっちの皿にはタコさんしか入っていないぞ?」と気づいたのですが、そのまま続けてみるとついに最後までそうだったというわけです。
形を見やすくするために広い皿に取りました。
こちらが左の皿・・・。タコらしきものばかり9個です。

こちらが右の皿・・・。タコ4個、その他6個です。

確率を計算してみよう
このようなことはどのくらい稀な現象なのか、確率を計算してみます。
1箱を合計してみるとタコ13個、その他6個という内訳になっています。これを2個ずつ取って交互に分けていくとき、片方の皿にタコばかり9個が入る確率を求めます。
確率というのは「全部の事象の起こる方法に対し、その現象が起こる方法が占める割合」という風に計算されます。
例題として、1,2,3,4と書かれたボールを右の皿と左の皿に2個ずつ分けるとして、1と2のボールが左の皿に載る確率を求めてみましょう。次のようになります。
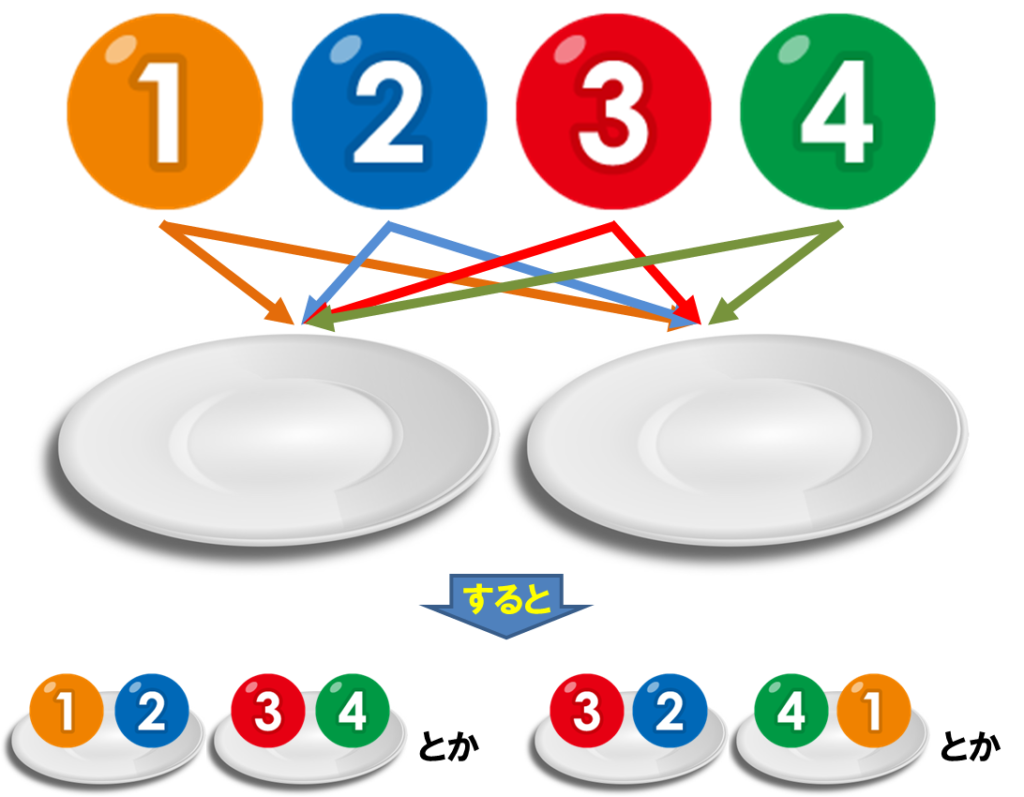
(1)ボールを1列に並べて、真ん中より左にあるボールを左の皿へ、真ん中より右にあるボールを右の皿へ載せると考えます。こう考えると、要するに「皿に載せる」ということは「並べ替える」ということと同じだと分かります。並べ替えた時点で皿に載せた結末まで見えるということです。

(2)ボールを1列に並べる方法は4×3×2×1=24通りと数えられます。
(2)そのうち、左側に「1,2」か「2,1」が並ぶ方法は、
1-2-3-4
1-2-4-3
2-1-3-4
2-1-4-3
の4通りだけです。
(3)したがって、左の皿に1と2のボールが載る確率は
4/24 = 1/6
と計算されます。
プッカの怪奇現象もこれと同様に考えていきます。まずプッカの1つ1つに番号をつけます。タコには1,2,3,…,13を。残りの6個には14から19までの番号をつけたとしましょう。これを1列に並べ、左から9個を左の皿に載せ、残り10個を右の皿に載せるという風に考えます。
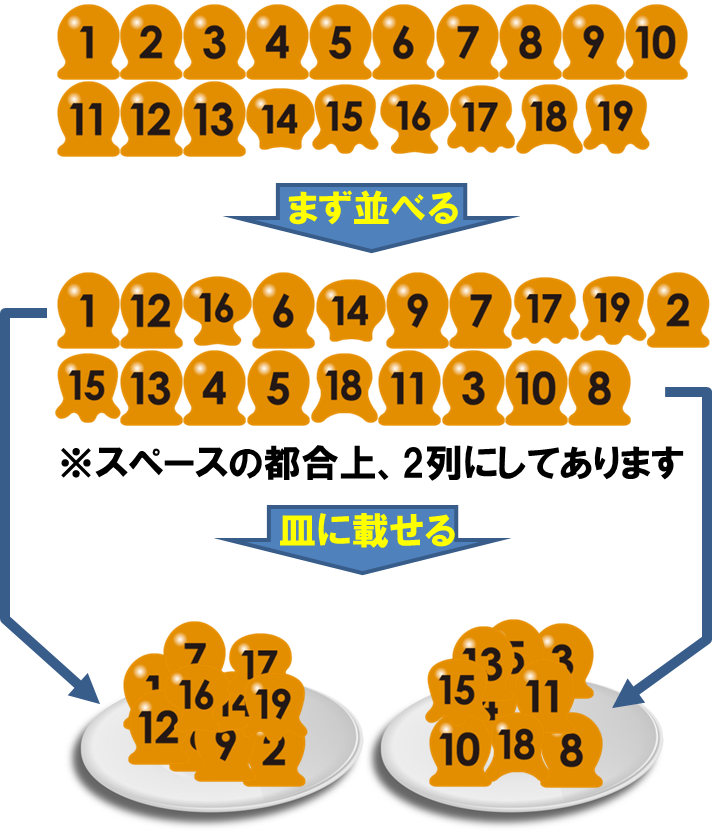
すると、全ての並べ替え方は「19個のボールを1列に並べる方法」と同じなので
19×18×17×…×3×2×1通り(これをAとします)
となります。
その中で、左から9個までが1~13のプッカで占められる方法は、
(13×12×…×6×5)×(10×9×…×2×1)通り(これをBとします)
となります。
ですので左の皿に9個のタコが載る確率は(ちょっと計算を飛ばしますが)
B/A = 60/323
となります。およそ19%の確率です。
これが珍しいことなのかどうかと考えると、うーん、まあ最初に「怪奇!」と思ったほど珍しくはないですね。でも「打率1割9分のバッターが思いがけずヒットを打った」と考えると、そこそこ珍しいような気もします。ちょうど2017年のカープの野間選手(打率.189)がヒットを打つ確率と同じです。もっと打ってほしいですね。
(2018年追記)こんなことを書いて1年後には、野間選手の努力と才能が開花し、初の規定打席到達、そして打率は.289と立派な成績になりました。また来年、更なる飛躍を期待したいと思います。その前にCS(クライマックスシリーズ)ですが。
そんなわけで、プッカで楽しく驚くひとときを過ごすことができました。近所の店にあまり売っていないのがつらいところです。
ほかのブログへ
↑クリックするといろんな科学ブログを探せます。ついでに「カガクのじかん」のランキングも上昇します(ありがとうございます)。






