
氷を水に入れると、浮力を受けて浮かびますよね。「氷山の一角」という言葉もある通り、氷は水面の上に少し顔を出した状態で浮かんでいます。ではこの氷が解けると、水はあふれてしまうでしょうか?

さっそくやってみました
こういうのは考えるのも楽しいのですが、実際にやってみるのが簡単でよろしいでしょう。私が試したところでは、1時間ぐらいで解けてしまいました。早送りの動画をどうぞ。
いかがなものでしょう?動画の水面をじっと見ていても、水があふれる様子がありませんよね。動画の最後にはコップの下の方が濡れていますが、これは空気中の水蒸気がコップの表面で冷やされて水滴になって、それがコップを伝って垂れてきたものですね。
つまり、「氷が解けてもコップから水はあふれない」と言えそうです。
なぜ?
まず前提として、「物体が受ける浮力の大きさは、物体が押しのけた水の重さに等しい」ということを理解しましょう。これを「アルキメデスの原理」といいます。ちょっと上手に表現できるかどうか自信がないのですが、次のように考えてください。図を見ながら文章を読んでみてくださいね。
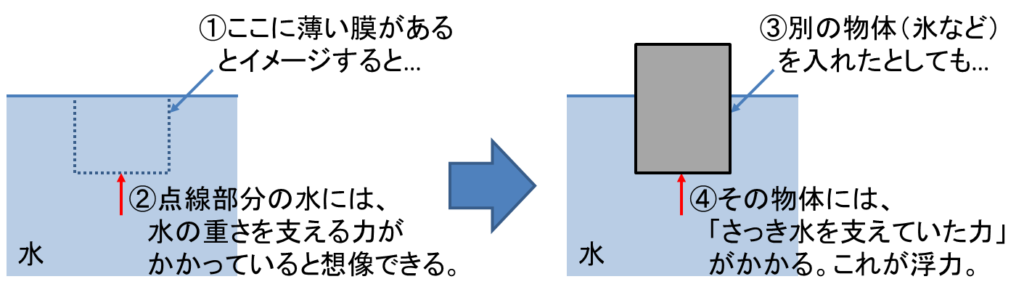
図中はマル数字になっていますが、文中ではカッコ数字にします→ 水の中に点線で適当な領域をつくります。この領域が薄い膜で包まれていると想像してみてください(1)。食品を包むラップのようなものを想像するといいですね。すると、膜で包まれた部分の水の重さを支える力が上向きにかかっているはずだ、と想像できます(2)。この力の正体は、この説明ではよく分かりませんが、「周辺の水が膜を押してくる力だろうな」という想像はできると思います。
さて、水のあった場所に別の物体(氷など)を入れたとしましょう(3)。この場合も、「周辺の水が膜を押してくる力」は同じようにかかります(4)。この(4)の力を浮力というわけです。ここまでの説明から、4の力は2の力と同じ大きさ、つまり「膜で包まれた水の重さを支える力」と等しいと言えます。
「膜で包まれた水」は、言い換えると「物体(3)が押しのけた水」と表現できますから、次のようにまとめられます。
まとめ(アルキメデスの原理): 水につかっている物体が受ける浮力の大きさは、その物体が押しのけた水の重さに等しい。
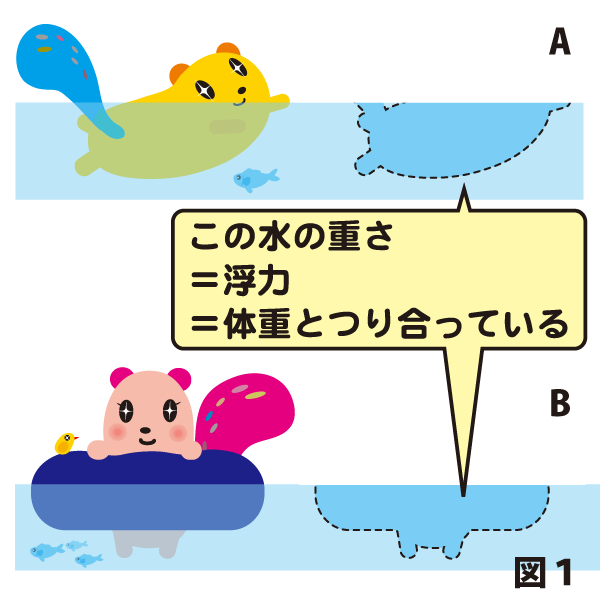
例えば図1Aのようにリスが水に浮かんでいる場合、「押しのけた水」とは図の点線で囲まれた部分のことです。リスの体重と点線部分の水の重さが等しいので、浮いているわけです。図1Bのように浮き輪を使うと、浮き輪がたくさんの水を押しのけてくれるので、体をあまり沈めなくても水に浮かびます。
ここで本題に戻りますが、次の図2のような状況で氷が解けると水面がどうなるかと考えると・・・。

氷が水に浮かんでいるということは、氷の重さは、氷がおしのけた水(図3の点線部分)の重さと等しいということですね。では、この氷が解けたらどれだけの体積になるでしょうか。
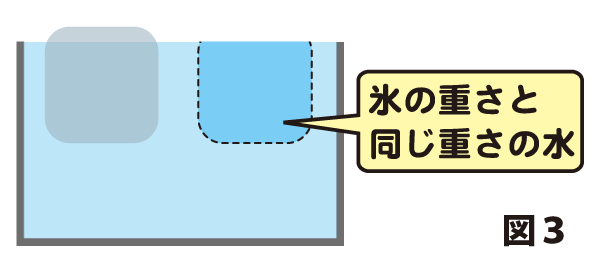
氷は溶けると水になりますね。「もとの氷と同じ重さの水」になるわけですから、その体積は・・・そう、図3の点線部分と同じ体積になります。したがって、氷が溶けた後のコップの様子は図4のようになるはずです。
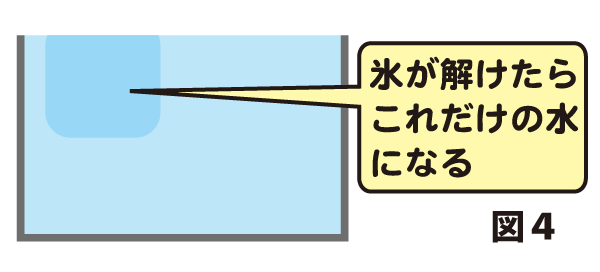
まあこんなわけで、氷が解けてもコップから水があふれてこないのですね。もし「海の氷山が解けたらどうなるのか?」などと考えたい人は、塩水で実験をしてみるとか、そもそも氷山は海に浮かんでいるのか、大陸の表面にくっついているのかどっちなのかを調べるなどしてみてはいかがでしょう。
出典
この記事はちゅーピー子ども新聞43号(2011年8月21日発行)7面に掲載した記事を加筆修正したものです。
ほかのブログへ
↑クリックするといろんな科学ブログを探せます。ついでに「カガクのじかん」のランキングも上昇します(ありがとうございます)。






