
センター試験お疲れさまでした!ざっと見て「ちょっとこの問題難しかったかもしれないな」と感じるものをいくつかピックアップして解説したいと思います。
問題・解答はいろいろな予備校が公表していますのでそちらでダウンロードしてください。例えば河合塾さんのサイトはこちらです。
2-2 ダイオードの整流作用・キルヒホッフの法則・電荷保存の法則
問の要約: 図2のような回路に図3のような電圧をかけたとき、点Pを流れる電流の時間変化を表すグラフはどうなるか。
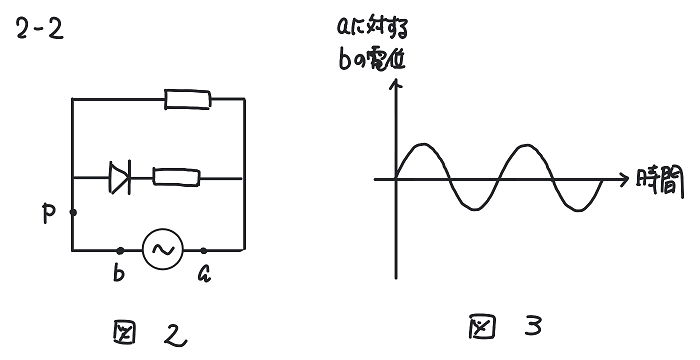
考え方
ダイオードが嫌いな受験生は多いと思いますが、ダイオードの働きについては問題文に詳しく書かれています。一言でいうと「整流作用」ですね。図2の左側が高電位の場合はダイオードは導線のようになり、右側が高電位の場合は電流が流れないということです。
そこをクリアすれば、あとは単に「電気回路だ。何を考えよう?」と基本に戻って考えればOKです。
えっ?電気回路と言えばオームの法則、合成抵抗、コンデンサー、インピーダンス・・・いっぱい法則があって大変ですって?
確かに色々な公式や法則は出てきますが、電気回路の分野で最も重要なのは
1. 電荷保存の法則(キルヒホッフの第1法則)
2. 閉回路を1周すれば電位差の和が0になる法則(キルヒホッフの第2法則)
の2つですよ。この2つが大黒柱のように電気回路の問題を支えています。そう考えると、次の図のように点Pを流れる電流を\(I\)として、上の抵抗を流れる電流を\(I_1\)、下の抵抗を流れる電流を\(I_2\)とすれば、
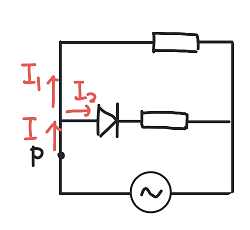
\(I = I_1 + I_2\)(電荷保存)
となることがすぐ分かります。あとは\(I_1\)と\(I_2\)をそれぞれ考えればいいですね。
\(I_1\)については「図3の電圧が抵抗にかかっている。抵抗においては電流と電圧の位相差はゼロ」ということから、\(I_1\)は図3と同じようなグラフになることが分かります。
\(I_2\)については、図の左側が高電位の時間帯(つまり電圧が正の時間帯)だけ\(I_1\)と同じ電流が流れますね。
以上のことを思いつけば、次の図のようなイメージで\(I\)を答えることができます。
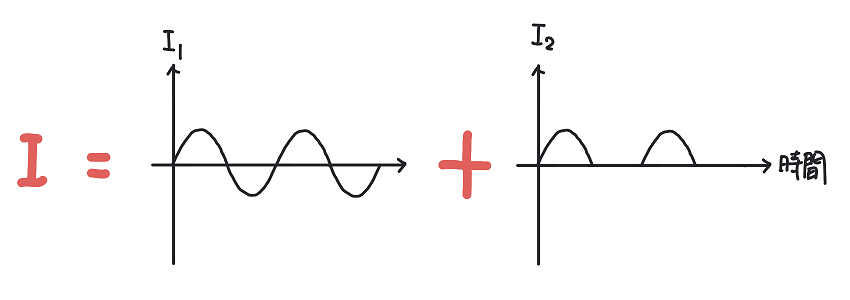
そのようなグラフは⑤ですね。
3-1 屈折時に位相が等しくなるのはどこまでか
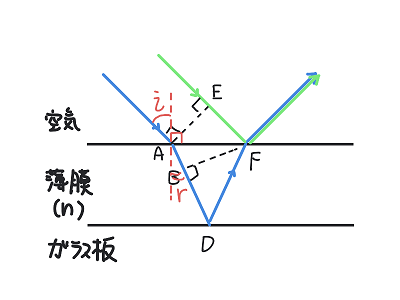
問の要約:次の図のように、空気(屈折率1)中を進む平行光線が、ガラス板の上に作られた平行薄膜(屈折率\(n\))に入射している。青線の経路は空気中から薄膜に屈折して進み、反射と屈折を経て空気中に出ていく。緑線の経路は薄膜の表面で反射する。この2つの光は点A・Eにおいて同位相であった。このとき\(n\)を図中の線分の長さ(ABやEFなど)で表すとどのような式になるか?
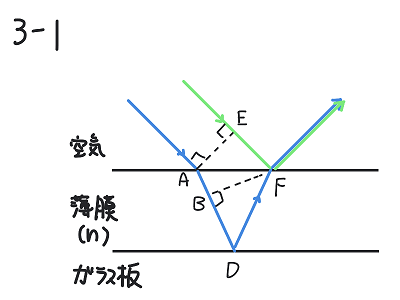
考え方①
問題全体のテーマとしては、このあと「平行薄膜での干渉」について問う内容になっていくのですが、この3-1に関してはそれ以前の内容で「ホイヘンスの原理」あたりで学びますね。ただ、それを思い出せるかどうかというのは人によって違ったと思います。「あっこの図はホイヘンスの原理で学んだ図だ」と思い出せるかどうか、です。
もし思い出したとすると次のような思考回路で解くと思います。
AとEが同位相なのであれば、同じくBとFも同位相になる(このことをホイヘンスの原理のあたりで学びます)。つまりABとEFに含まれる波の個数は同じだ。つまり空気中の波長を\(\lambda\)、薄膜中の波長を\(\lambda’\)とすると、
\( \frac{\mathrm{AB}}{\lambda’} = \frac{\mathrm{EF}}{\lambda} \)
となる(経路の長さを波長で割れば波の個数になりますから)。
ところで\(n\)と波長の関係は、屈折の法則(というよりも\(n\)の定義)から
\(n = \frac{\lambda}{\lambda’}\)
なので、この2つの式を組み合わせると
\( \frac{\mathrm{EF}}{\mathrm{AB}} = \frac{\lambda}{\lambda’} = n\)
となる。よって①ですね。
考え方②
先ほどのような考え方は、思いつかなかったらどうしようもないという弱点がありますね。しかしそんな場合でも「\(n\)って屈折の法則で出てくるものなんだから、とりあえず屈折の法則からスタートしてみよう」と考えてみることができます。
その場合は、次の図のように入射角を\(i\)、屈折角を\(r\)として何となく屈折の法則を立ててみます。
\(\frac{\sin{i}}{\sin{r}} = \frac{n}{1}\)
この左辺を何とかして線分の長さで表すことができればいいですね。sinってそもそも長さの比で表せるわけですから、なんとかなるはずです。
図をよく吟味すると、次の図のように\(i\)と\(r\)が存在しているのが分かりますから、
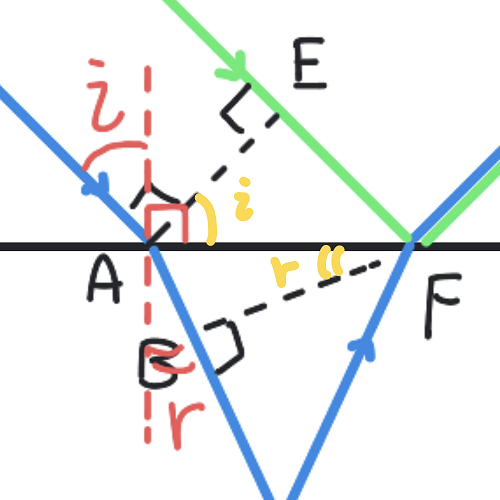
\(\frac{\sin{i}}{\sin{r}} = \frac{\mathrm{AE/AF}}{\mathrm{AB/AF}}\)
という風に線分の長さで表せることが分かります。右辺は\(\frac{\mathrm{AE}}{\mathrm{AB}}\)になりますので、これで答えが①と求められました。
こちらの解き方の方が、思いつきの部分でのハードルは低いのではないかと思います。ちなみに最後のあたりのプロセスはホイヘンスの原理を初めて習う場合と同様な式変形です。
3-3 単振動の\(x\)-\(t\)グラフを式で表せ
問の要約:音源の位置\(x\)と時刻\(t\)が次のグラフのように単振動しているのであるが、これを式で表すとどうなるか。
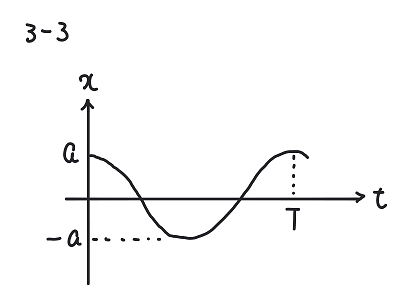
考え方
これはもう見たまんまで「振幅\(a\)で周期が\(T\)でコサインのような関数」なので(角周波数\(\omega = 2\pi/T\)に気をつけて)、
\(x = a\cos{\frac{2\pi}{T}t} \)
で終わりにしたいところなのですが、選択肢がすべてsinなんですよね。ちょっといやらしいですね。選択肢の④か⑥となりますが、どっちでしょう。
もちろんここで
\(\sin\left(\theta + \pi/2\right) = \cos{\theta}\)
\(\sin\left(\theta – \pi/2\right) = -\cos{\theta}\)
ということを、単位円を描くなどして導出できればOKです(または公式丸暗記でもOK)。そうすれば④と分かりますね。ただ、公式丸暗記だと焦っているときに逆の方を思い出したりしそうですよね。なのでその場で導出する方をお勧めしたいですが、さらにそれも焦って図がうまく描けない!などの場合は、さらに次の策として「選択肢の\(t\)に適当な値を代入してみる」というのもお勧めです。
今の場合なら\(t=0\)を代入してみると、④は\(x=a\sin{(\pi/2)}=a\)となりますが、⑥は\(x=a\sin{(-\pi/2)}=-a\)となります。与えられたグラフはもちろん、\(t=0\)においては\(x=a\)ですので、④が残ります。選択肢がある場合に特有の消去法ですが、こういう思考回路もありですね。
4-2 減速する電車内でボールを放すとどうなるか?
問の要約:次の図のように電車が一定の加速度\(a\)で減速している。このとき電車内の少年がボールを静かに放した。このボールを電車内で観測したとき、ボールの軌道はどのようになるか。
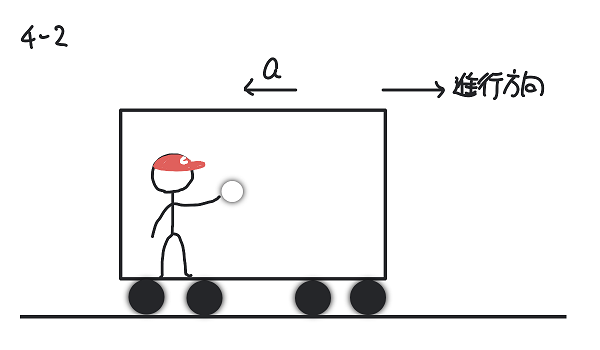
考え方
「地面に対して加速度をもって運動する観測者」が力学の法則を立てたい場合は、「慣性力」という力がかかっていると思うことにすればOKです。ちょっと回りくどい言い方になりましたが、今回の場合は、電車内の少年がボールを観測すると、ボールには重力のほかに「慣性力」という力がかかっているように見えるということです。
慣性力は、観測者の地面に対する加速度の反対向きに、大きさ\(ma\)です(\(m\)はボールの質量)。ですからボールには次のように2つの力がかかり、その合力は斜め右下向きに一定の大きさとなります(図中の青矢印)。この合力のことを「見かけの重力」と呼ぶこともあります。
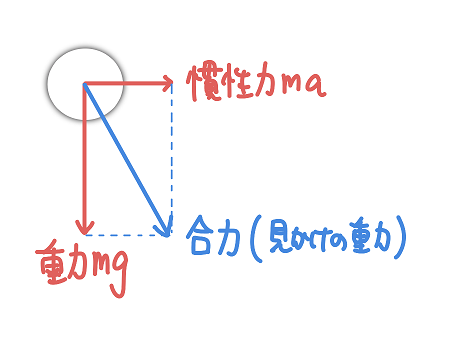
さてこの状況でボールを放すとどうなるでしょうか。初速度0で、右下向きの合力を受けながら運動するので、ボールは合力の向きに加速していきます。よって合力の向きに運動していきます。ですので⑤ですね。
まあ力の図示まで済んだら「初速度が0なんだから見かけの重力の向きに自由落下していくよね」と軽やかに考えることができれば気持ちが楽だったでしょうね。
5-3 \(p\)-\(V\)図で与えた熱サイクルを\(p\)-\(T\)図にするとどうなるか
問の要約:次の図のような熱サイクルがある。この過程A→B→C→D→Aの温度と圧力の関係を表すグラフはどうなるか?
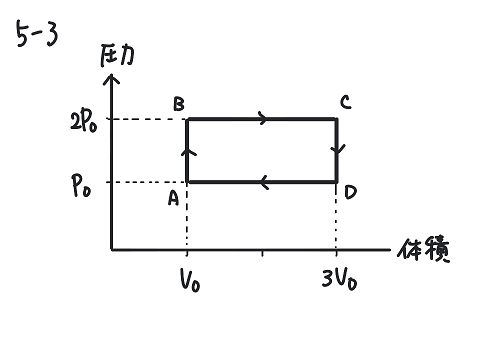
考え方
熱力学の分野は、電気と似て「用いる公式が結構多い」という特徴があると思います。そのため頭がゴチャゴチャになりやすいのです。しかし上に書いたとおり、例えば電気回路の分野なら柱になるのはたった2つの法則です(他の公式類が不要という意味ではなく、この2つが柱だという意味です)。同様に熱力学の分野も、大黒柱になる法則はわずかです。本問はそのうちの1つ「状態方程式」を使うと解ける問題ですね。
温度\(T\)と圧力\(p\)の関係をグラフにするというのは、人によってはあまり慣れていないかもしれませんが、「A→Bのとき\(T\)と\(p\)はどういう関係になるのかな?」と1つずつ考えていけばよいわけです。その考えるために必要な法則を大黒柱から探してみると、すぐ「状態方程式だよなぁ」と思いつくというわけです。
A→B: 体積\(V\)が一定ですので、状態方程式「\(pV=nRT\)」を思い浮かべると、\(p\)と\(T\)は比例関係だなと分かります。この時点で③と④は消えますね。
B→C: 圧力\(p\)が一定ですので、\(p\)-\(T\)のグラフでは真横向きになります。この時点で①と②も消えますね。ちなみに\(V\)が3倍になりますので、最終的には\(T\)が3倍になります(状態方程式より\(V\)と\(T\)が比例するためです)。
C→D: これはA→Bと同様に\(p\)と\(T\)が比例関係になりますので、残った⑤と⑥のうち⑤はダメと分かります。変化の直線を延長すると原点を通らないためです。
ここまでで⑤となりました。
まとめのコメント
毎年毎年、新しい入試問題が作られます。再来年からは入試制度も大きく変わります。ですが結局のところ、物理の入試で問われるのは「物理法則を理解しているか」「物理法則を使えるか」ということなんだと改めて感じる問題でした。結局はそのような力をもった人材が育って欲しいという国の意識の表れなのでしょうし、私個人としても大いに賛同するところです。
学校でも塾・予備校でも様々な問題演習をすると思いますが、その問題演習はあくまでも「初めて見た問題であっても、知っている法則を正しく適用すれば解けるということを確認する」ために行うべきであって、「似たような問題が出たらパターン認識で解けるだろうウヒヒ」という目論見で演習をするのは物理の本質を外している・・・と常々思っていますが、今回の出題を見てもその見立ては間違っていないだろうと思います。
受験生一人一人は、大学入試が終われば、今まで身に付けた物理にさらに上乗せして物理学を修得し、その知見を持って世の中に貢献する人材になっていくのです。そういった未来に貢献できるような物理の力を受験生の皆さんには身に付けていただきたいと思いますし、私は指導者の一人として受験生をそのような未来に誘っていきたいと改めて思いました。






