
【管理人より】私が勤務する塾の高3生向けの記事です(2015年1月1日公開)。他の方にも理解していただけるように書きますが、ある程度は「物理」の知識が必要かもしれません。
受験生の皆さん、受験前の忙しい時期にアクセスありがとうございます。日頃からあまりしゃべるのが上手でなく、伝え切れていないことがあるように思っているので、このような記事を書こうと思いました。
センター試験が近いことから、学校でも塾でも高3担当の先生から受験生の皆さんにあてたメッセージを聞いたり読んだりしたと思います。私からは次のようなメッセージを送らせてもらいました。
赤い星、青い星、夜空にはたくさんの星がありますね。クールに見える青い星は、赤い星より4倍ぐらい高温です。もっと熱い星は目では見えませんので真っ暗です。あなたの温度は、あなたが一番よく知っていますよね。何色でもいい、「じぶん色」で精一杯輝いてください。
この記事では、もう少しいろいろ補足説明を試みたいと思います。
光の「色」とはなんだ
そもそも星から出る光の「色」って何なのでしょう。
高3生なら覚えていますよね。光(=可視光線)は「電磁波」という波のうち、特定の波長領域を指すもので、色はその波長で決まっています。波長が長い光は赤く見え、波長が短い光は青(紫)に見えます。赤よりももっと長い波長の電磁波は赤外線、もっと長いと電波といいます。紫よりもっと波長が短いと紫外線、もっと短いとX線、γ線といいますね。これは「波動」の単元で習う知識です。図中に出てくる「ナノメートル」とかについては「小さな量のあらわしかたのお話」などご参照ください。
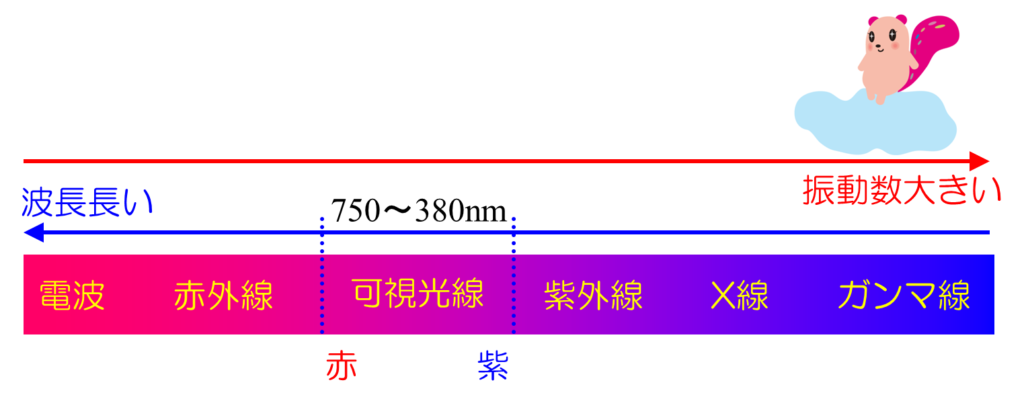
星から出る光は、例えば赤い星だからといって赤の波長の電磁波だけが出ているわけではなくて、赤を中心としてある程度の範囲の波長の電磁波が混ざっています。例えば太陽光は通常「黄色」に分類されます(スペクトル型がG型→wikipedia)が、太陽光って何となく白っぽいですよね。これは赤から紫までいろんな光が混じっていることを表しています。白い光を波長ごとに分解すると虹のような色の帯ができますよね(ちなみに虹のでき方については以下の「虹のお話」をどうぞ)。これも「波動」の単元で習いますね。
電磁波の色はどうやって決まるか
電磁波の色はどうやって決まるのでしょうか?それ以前に、電磁波ってどうやって発生するのでしょうか?
それを理解するための第一段階として、まず次の動画を見てください。
およそ次のようになっています。
- 電磁波とは「電場と磁場の振動が伝わっていく波」である。
- 電荷に電気力線がついてくる。
- 電荷が加速(or減速)すると、電気力線がついてこようとするため、「電場の波」が生じる。
- 電場が波になるときは同時に磁場も波になるので、すなわちこれが「電磁波」である。
ちなみに念のためですが、「電場の波」とは、次の絵の赤線のことです。この赤線が、水の波でいうところの「波紋」に相当します。このあたりは確か「磁気」の単元で学びますね。
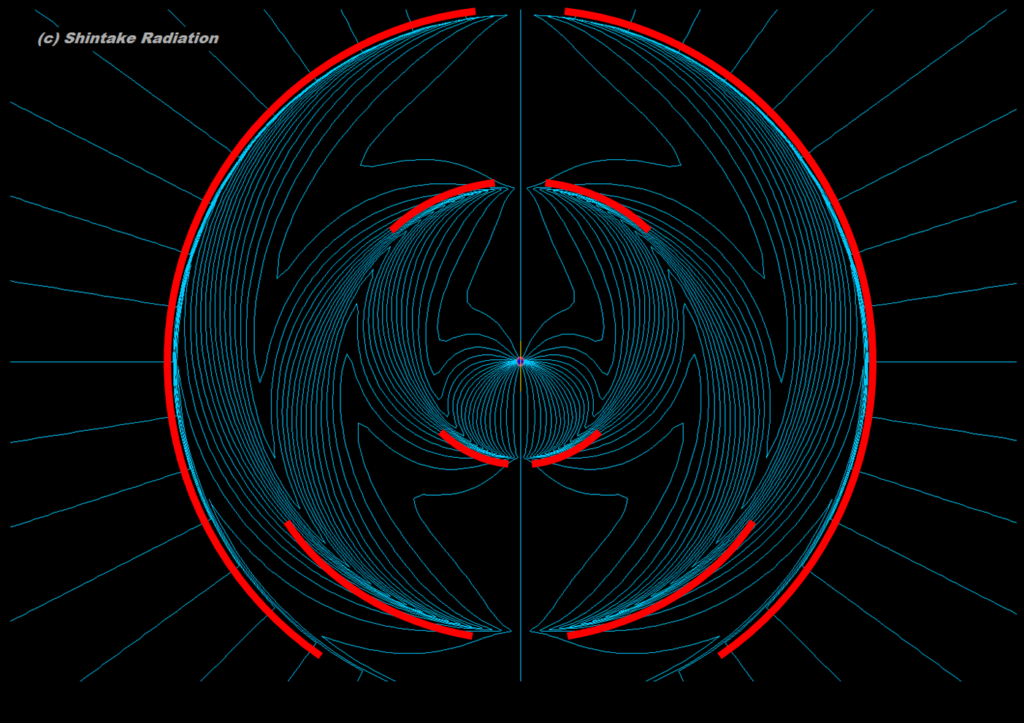
さてそうすると、赤い色の可視光線を出すには、電荷(電子など)を「赤い色の可視光線と同じ振動数」で振動させればいいと分かります。例えば赤の波長を750nmとすると、振動数νは次の式で求められますね(「波動」の単元で最初に習う内容です)。
ν[赤] = c/λ = 3.0×108/(750×10-9) = 4.0×1014[Hz]
となります。もし紫色の光を出したいのなら、紫の波長を400nmとして
ν[紫] = c/λ = 3.0×108/(400×10-9) = 7.5×1014[Hz]
という振動数で電荷を振動させればよいと言えます。ちょっと数字が大きすぎてイメージが難しいですが、まあ要するに「光を出すために必要な電荷の動きとしては、赤よりは紫の方が2倍ぐらい忙しい」というイメージです。
ちなみに「単振動」の単元で学んだ知識を活かすと、単振動における最大の速さは
v[最大] = Aω
と表せますので(Aは振幅、ωは角振動数)、上記の「2倍ぐらい忙しい」というのは「速さがおよそ2倍」と言い換えることもできます。
星から出る光の色はどうやって決まるか – その前に「星の温度」
徐々に本題に近づきます。星から出る光の色はどうやって決まるか、です。
まず基本的な知識として、太陽などの星は高温のガスの塊です。なんで高温になるかというと、まずは「ぼわ~っと広がっていたチリが小さくまとまるときに放出される位置エネルギー」に起因します。詳しく書くと次のようなプロセスです。
- そもそも星の原料となるチリ(大半が水素)は、最初は宇宙空間にぼわ~っと広がっている。
- それが万有引力によって引き合い、小さくなる。
- そのとき「万有引力による位置エネルギー」が減少するので、その分チリの運動エネルギーが増える。
- チリの運動方向はランダムなので、この運動エネルギーはすなわち熱エネルギーであって、運動エネルギーに比例した絶対温度を持つと言える。
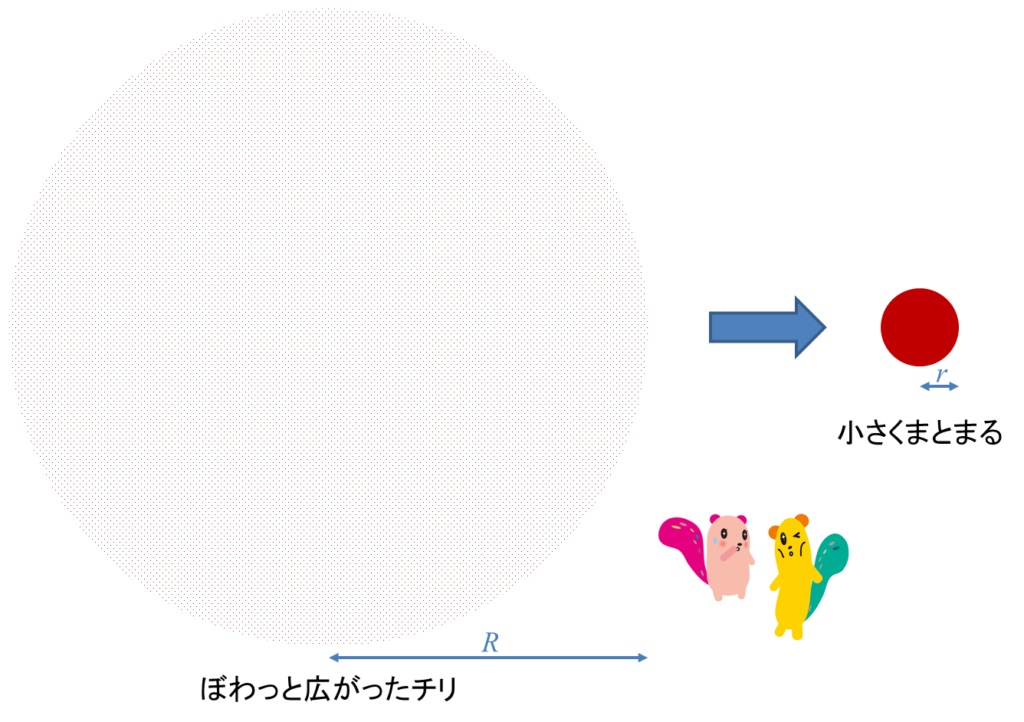
ちょっと計算してみましょうか。距離Rぐらいの空間に散らばっていた質量Mのチリが集まって、半径rの球体(例えば太陽)になったとしましょう。このとき減少する「万有引力による位置エネルギー」-ΔEは、だいたいこのぐらいになると思われます。Gは万有引力定数です。
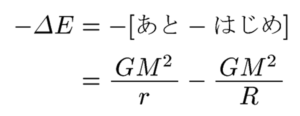
さらに、rに比べてRが非常に大きいと仮定すると(多分そうなっているでしょう、宇宙空間はものすごく希薄ですから・・・)、
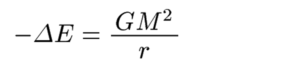
となりますね。これがチリの熱運動の運動エネルギーになっているとしますと、絶対温度をT、チリの粒子数をNとおいて、
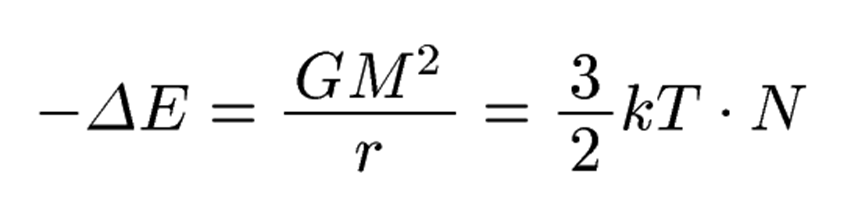
と表せます(kはボルツマン定数です)。ちなみに太陽のほとんどは水素でできていますので、
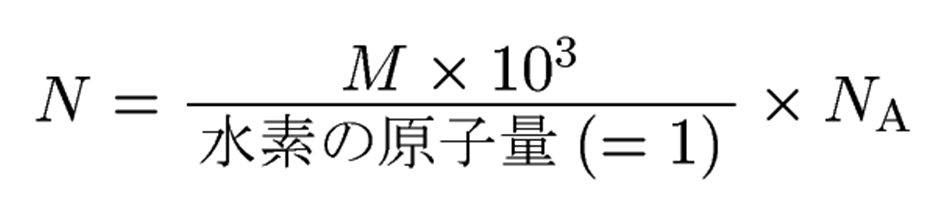
となりますね。NAはもちろんアボガドロ数です。分子の「×103」は、キログラムで表したMをグラムに直すためにかけました。
太陽の質量や半径はwikipediaなんかで調べるといいでしょう。ボルツマン定数は物理の教科書の巻末に載っていますが、ど忘れしたらwikipediaをどうぞ。
結果的に、絶対温度Tは次のようにして求められます。
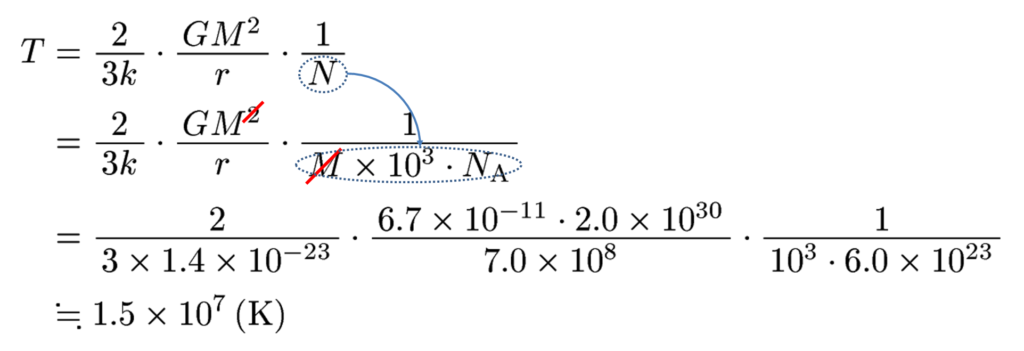
まあだいたい1500万度ぐらいですね。計算の最初のあたりが結構おおざっぱですので、「1000万度台」ぐらいに思っておくといいでしょう。こういうのを「オーダー計算」とか「桁の見積もり」といいます。
ちょっと大変でしたが、万有引力、力学的エネルギー保存則、気体の分子運動論の知識を組み合わせて、こういう大まかな計算ができました。
このぐらいの温度になると、水素原子は電離してしまって、電子と水素原子核に分かれます。なぜって?「ボーア模型」の単元で算出しましたよね。水素原子の基底状態におけるエネルギーは-13.6[eV]です(覚えなくてもいいと思いますが)。つまり基底状態にある電子1個を取り去るには13.6[eV]のエネルギーを加えればいいわけです。このエネルギーを水素原子同士の衝突によってまかなうとして、水素原子の温度T’を見積もると、次のようになります。
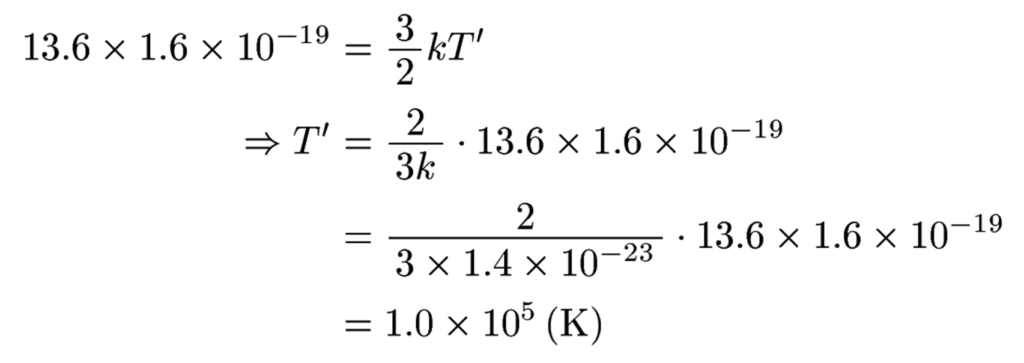
まあだいたい「10万度」ですね。だから1000万度もあれば十分に電離してしまうと考えられます。
星から出る光の色はどうやって決まるか – その前に「核融合反応」
星の色の話とは直接関係しないのですが、星の中心で起こっている「核融合反応」についても触れておきます。引き続き、太陽を例にとって考えてみます。
前述のように、チリが集まってきて「万有引力の位置エネルギー」を解放した・・・と考えてみたわけですが、そのエネルギーが光のエネルギーに変わっているとしましょう。太陽が放出しているエネルギーは、地球近辺での測定値(人工衛星で測定できます)と距離が分かれば算出することができて、wikipediaによれば3.8×1026J/sぐらいだそうです。では、開放された「万有引力の位置エネルギー」を、3.8×1026J/sの割合で消費していくと何年もつのか計算してみましょう。
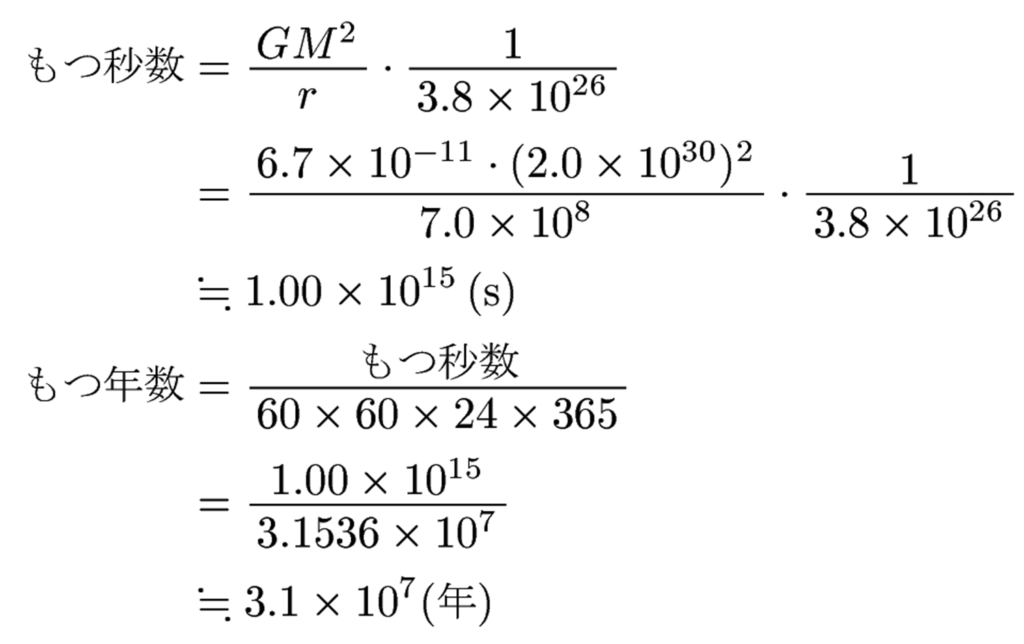
おお!3.1かける10の7乗年、つまり3100万年。長い!と思ったかもしれませんが、地球の年齢は45億年ぐらいだと考えられています(wikipediaにあるように、地球や月で見つかっている岩石の年齢から算出しています)ので、太陽のエネルギーが3100万年で枯渇してしまってはおかしいですね。
つまり、太陽光の主たるエネルギー源は「万有引力による位置エネルギー」ではないわけです。何なのでしょう?
種明かしをすると(といっても皆さんご存じだと思いますが)、太陽中心における「核融合」のおかげです。核融合によって水素原子核がより重い原子核(とりあえずヘリウムですが)に変わり、そのとき起こる質量欠損がエネルギーに変わるのですよね。これは物理の最後の「原子核」という単元で学びましたね。
ちなみに、核融合が開始するためには、2つの水素原子核の間に核力(=「強い力」)が働くぐらい近距離(2×10-15mぐらい)に近づかないといけませんが、そのために必要なエネルギーを「運動量保存則」「力学的エネルギー保存則(クーロン力使用)」で求めてみると、1000万度では全然足らない・・・というのを「原子核」のテキストの最後の問題で計算してみましたよね。どうなっているかというと、これは「トンネル効果」という、高校生はあまり深入りしない内容が関係しています。物質波の存在確率が壁から浸みだして・・・という話です。より興味のある人は、大学で少し「量子力学」をかじってみるといいと思います。

日本評論社 シリーズ・現代の天文学 7巻「恒星」(野本憲一ほか)p.150
お待たせしました!星から出る光の色!
まあそんなこんなで、太陽などの星の中では核融合反応が起こっていて、それで得られたエネルギーは水素原子核やヘリウム原子核の熱運動の運動エネルギーになります。これらの原子核はプラスの電気を持っていますから、これらの原子核が互いにぶつかったりして方向転換(=加速)すると、上の動画で説明したように「加速する電荷から電磁波が出てくる」という事態が起こります。単振動のような動きをしていると仮定すると、速度が速いほど振動数も大きくなりますから、次のような図式が成り立ちます。
温度が高い
→原子核が飛ぶ速度が速い
→振動数が大きい(単振動だと仮定)
→波長の短い電磁波が出る
実際に、どのくらいの温度だったらどのくらいの波長の電磁波が多く出るのか?というのは少し難しい問題でして、量子力学、統計力学、熱力学あたりを学ばないと辛いでしょうね。次の写真は私が使っていた教科書のページです。かろうじて「hν」というなじみのある表記を見つけることができますが、それ以外は少し難しいですね。ちょっとかじってみたい人はここ(琉球大学前野先生による解説)からウロウロしてみるといいかもしれません。ちなみに「黒体輻射」という現象です。
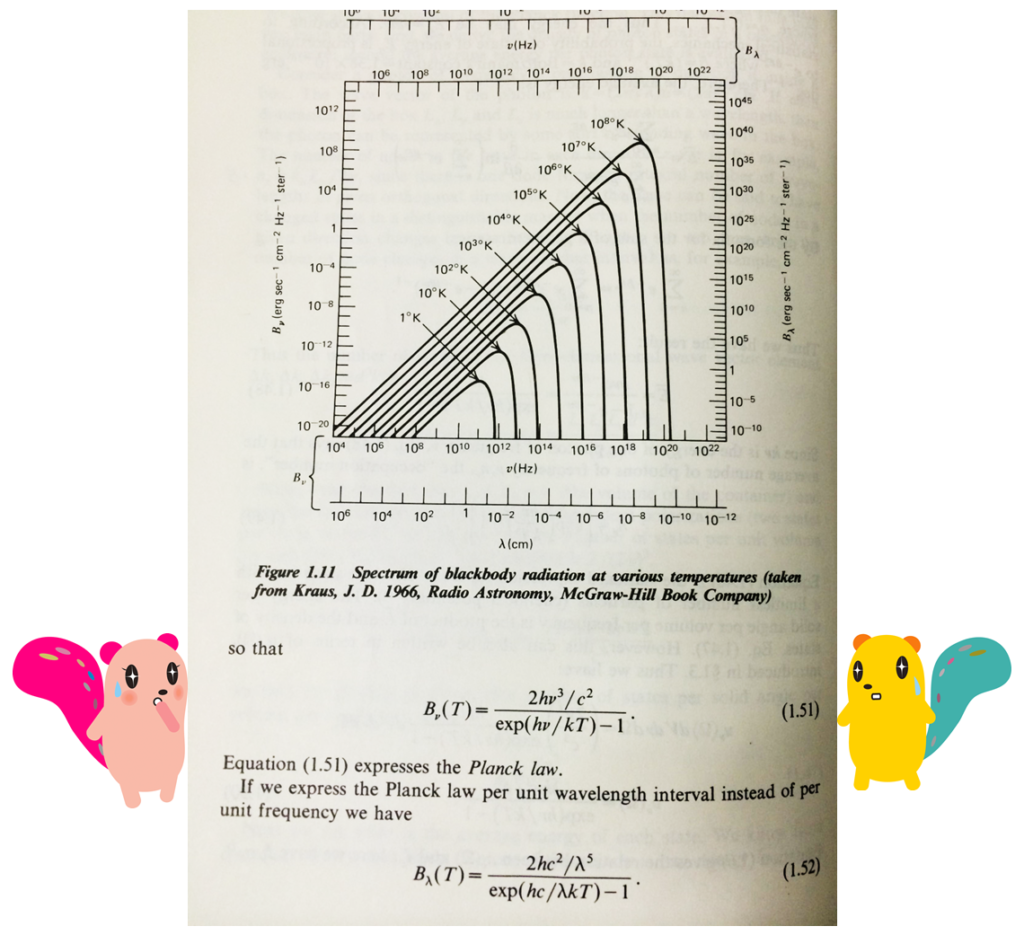
Wiley-Interscience Radiative Processes in Astrophysics (G.B. Rybicki & A.P. Lightman) p.22
ちなみに、星の表面温度と色(スペクトル型)の関係はここなどで見ることができます。太陽のように黄色の星は約6000度。赤い星(=波長が長い)は約3000度。青白い星(=波長が短い)は約10000~20000度。
この調子でいくと、もっと温度が高ければ、目で見えない紫外線やX線の星になるのではないかと思われますね。実際その通り・・・というとちょっと言い過ぎな面はあるのですが、紫外線やX線が主に放出されている場所は、可視光線が主に放出されている場所よりも高エネルギーの粒子がたくさん居るのは間違いありません。例えば太陽だと、太陽表面は6000度ぐらいですが、その上空の「コロナ」という領域は100万度ぐらいです(これなどを参照)。コロナからは活発にX線が放出されています。
冒頭に戻ります
さて、受験で忙しいというのにこんな文章に付き合ってくれてありがとうございます。冒頭のメッセージに戻りましょう。
赤い星、青い星、夜空にはたくさんの星がありますね。クールに見える青い星は、赤い星より4倍ぐらい高温です。もっと熱い星は目では見えませんので真っ暗です。あなたの温度は、あなたが一番よく知っていますよね。何色でもいい、「じぶん色」で精一杯輝いてください。
どうですか?この記事を読む前に比べて、違って感じられませんか?もし何か少しでも違っていたら、それが「分かる」ということだと思います。それは、しんどいながらも物理を最後まで履修してきた皆さんだからこそ得ることができた、「世界を見る新しい目」です。
今回利用した知識は以下の通りです — 力学(運動量・エネルギー・単振動・万有引力)、波動(波長と振動数の関係)、熱力学(分子運動論)、電磁気(クーロン力・電気力線・電磁波)、原子核(物質波・ボーア模型・電子ボルト・質量エネルギー・核融合反応)、モル(←これは化学ですが)。皆さんは、これらの知識がない人が持っていない「新しい目」を手に入れました。
もちろん、トンネル効果や黒体輻射を理解するには、あと2年程度は物理の勉強が必要ですし、全員がそこまでするわけではないでしょう。でも、ここまでで分かってくれると思いますが、大学で「専門知識を学ぶ」ということは、皆さんそれぞれが世界で生きていくための「新しい目」「新しい力」を手に入れるということです。自信と希望を持って進学してほしいと思います。
「センター試験まであと○○日」とかいうことは、もちろんそういう関門をクリアするためには意識すればいいと思いますが、センター試験が何かのゴールではありませんよね。2次試験も別にゴールではありません。大学に入って、シューカツをくぐり抜ければゴールでもありません。これだけ変化の激しい世の中ですから、常に前のめりに。重心がつま先を越えると転びそうになります(重心?何のことだ?と思った人は「転がる=転ぶのお話」へGo!偶力の話ですね)。でも転ぶ前にもう一歩踏み出すんですよ。そうやって走って行けたら、人生楽しいんじゃないかと思います。
そんなことが言いたくて、応援メッセージを書きました。
では皆さん、ひとまずはセンター試験で力が出せるように、体調に気をつけて、演習や復習の計画もきちんと実行してください。
ついしん
受験が近いとか何とかいう理由でやたら盛り上がる必要は本来はなくて、静かに着々と準備を進めることの方が重要ですよね、という気持ちもあります。やたら盛り上がる人は、星にたとえると真っ赤に燃えている低温の星。静かな人は暗くて高温の星です。と私は思います。センター試験までの残り○○日に何かが存在しているのではなくて、高校に入学してからの1000日の方に何かが存在しているはずです。
【おまけ】万有引力による位置エネルギーの導出
星から出る光の色はどうやって決まるか – その前に「星の温度」 のところで、半径Rの球状に分布した質量Mのチリの「万有引力による位置エネルギー」を-GM2/Rとしました。本来は、N個あるチリの「任意の2つの粒子間にたくわえられる位置エネルギー」を足しあわせる必要があります。
N個のチリに1, 2, 3, …, Nと番号をつけて、それぞれの質量をm1, m2, … のように表すとします。また、i番目とj番目のチリの距離をrijと表すとします。すると、ここに蓄えられている位置エネルギーUは、形式的に次のように表すことはできます。
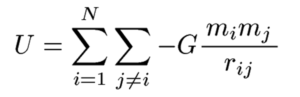
ですが、まあこれじゃ何言ってるか分かりませんよね(汗)。なので、「分母はまあだいたいRぐらいだろう」「分子はM2ぐらいだろう」という雰囲気をつかんで表現したのが、上の記事中の-GM2/Rという式なんです。こういう、「だいたい桁がどのくらいかを見積もろう」という姿勢を「オーダー計算」などと言いますが、これはあまり高校時代は触れることのない概念ですよね(私のクラスに在籍していると何度か出てきたと思いますが・・・)。そういうのを学ぶと、また世界の見え方が変わりますよ。
ところで、もしもこのチリの球体が密度一様だとすると、こんな風に計算することはできます。密度をρとします。半径Rの球体の中に「半径xの小さな球(青)」と、「その外側に薄皮のようにはりついた、厚みdxの球殻(オレンジ)」をイメージします。
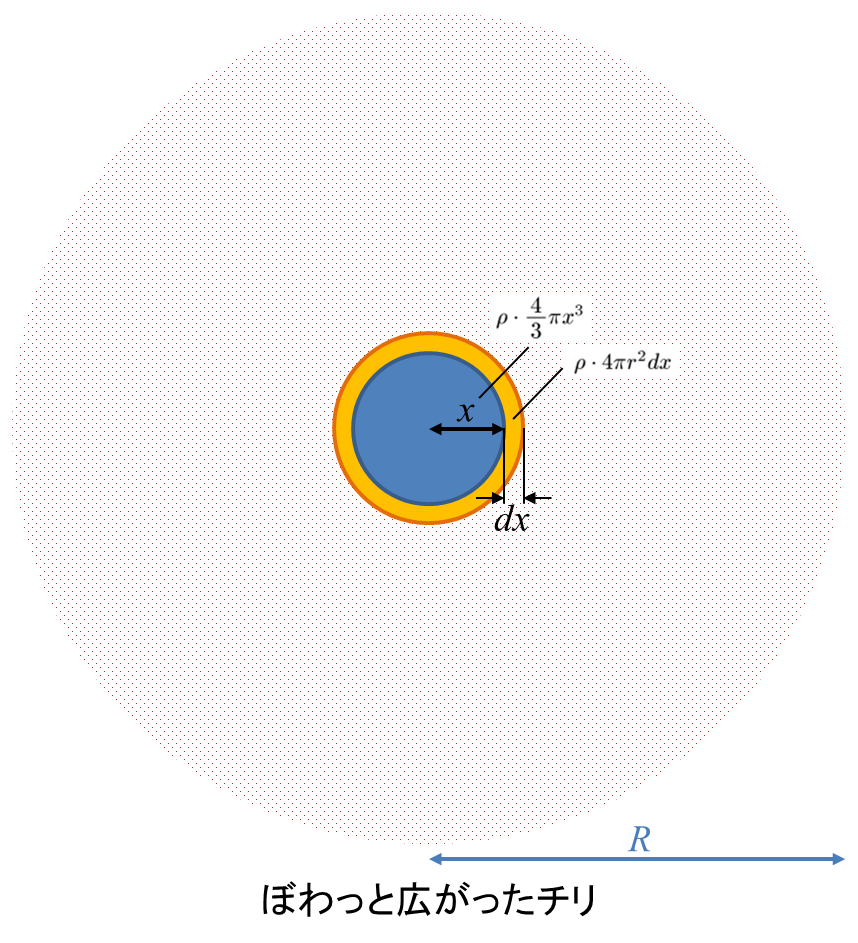
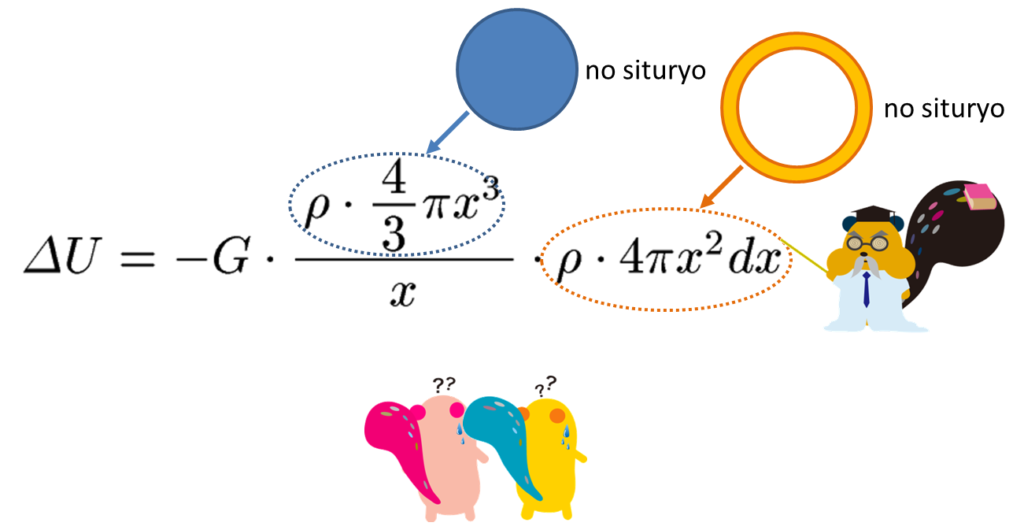
すると、オレンジの球殻の位置エネルギーΔUは次のように表すことができます。ウッとひるんでしまいそうになりますが、単に「●の中心から距離xのところに◎が居る」ときの位置エネルギーの式ですよね。
これをx=0からx=Rまで足しあわせればよい・・・すなわち積分すればいいですね。こういう計算は「コンデンサーの極板間引力」でも行ったことがあります。
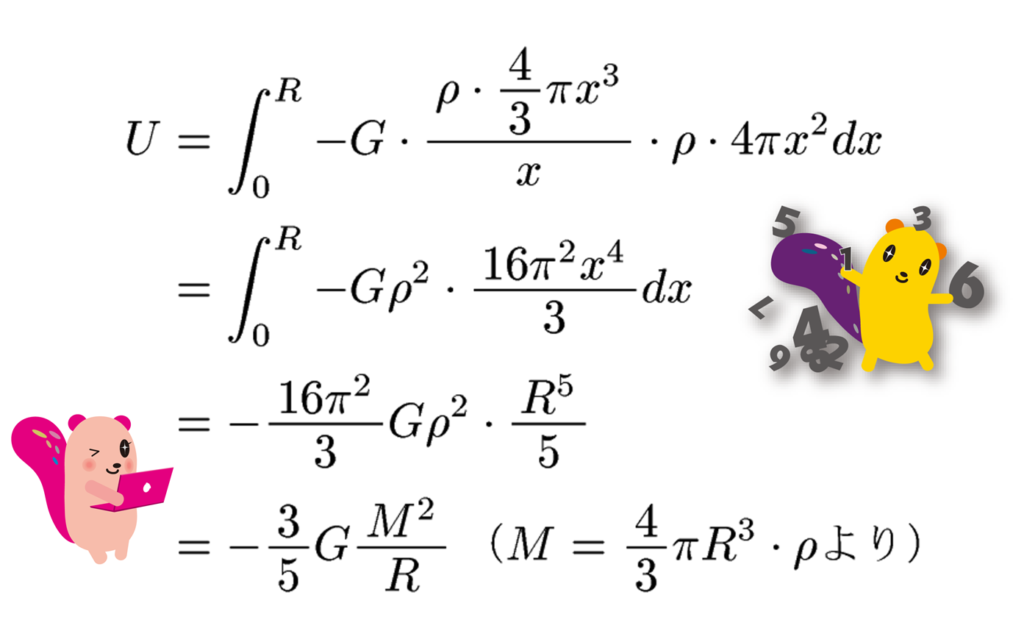
結果的に、3/5という係数がつきましたね。密度が一様だとこんな感じになるというわけですね。実際には、「ぼわっと広がったチリ」なら密度が一様とみなせると思いますが、太陽ぐらいのサイズに縮まった場合(半径rの場合)には一様でない密度分布が生じそうですので、それはまたそれで計算しないといけないという・・・。でも要するに「だいたいこのぐらい」という目的は達成できていると思います。
参考
- 波動くん(動画中で用いた電気力線描画ソフト)
ほかのブログへ
↑クリックするといろんな科学ブログを探せます。ついでに「カガクのじかん」のランキングも上昇します(ありがとうございます)。






