高校で物理を学びますと「重力加速度」というものを習います。
これは「\(g\)」という記号で表され、値はおよそ9.8m/s\(^2\)です。
この\(g\)のそもそもの意味は
「落下する物体の速さは、毎秒9.8m/sずつ速くなる」
ということです。初速度0で物体を落として1秒経つと速さは9.8m/sに、2秒経つと速さは19.6m/sに・・・という具合にどんどん速くなっていくのです。
落下距離の公式は便利だけど9.8が面倒
もっと便利なのは落下距離を表す公式ですかね。初速度0で物体を落として\(t\)秒後の落下距離\(h\)は
\(h [\textrm{m}] = \frac{1}{2}gt^2\)
と表されるのです(「公式」と書きましたが、物理を履修中の高校生はこの式をいきなり無批判に覚えようとしてはいけませんよ。成り立ちを理解しましょうね)。何が便利かというと、この\(t\)の部分に数字を入れると\(t\)秒後の落下距離がコロンと出てくるのです。例えばもし「3秒で何m落ちるのかな」と思ったら、\(t\)に3を代入して
\(h = 9.8\times 3^2/2 = 88.2/2 = 44.1[\textrm{m}] \)
のように計算できるというわけです。
ただ、電卓がないとちょっと面倒かもしれませんね。その元凶(?)は、\(g\)の値が「9.8」などという微妙に細かい値だからです。
では、もし\(g\)の値がスッキリ10だったら・・・?
計算は超絶ラクになります。例えば先ほどの計算は
\(h = 10\times 3^2/2 = 90/2 = 45[\textrm{m}] \)
のように暗算でできます。要するに「\(h=5t^2\)」となるので、最初の1秒で5m、2秒で20mのように本当に計算がラクですね。
ですから、ざっと概算する目的の場合は、いちいち\(g = 9.8\)などという数値を使わずに、\(g\)に10を代入しておけばいいでしょう(凡人の発想)。
いや待て、いっそ何とかして\(g\)を10にする方法はないでしょうか?(天才の着想)
こうすれば10にできる!(天才)
ある日、愛読させていただいている「アジマティクス」の筆者である鰺坂もっちょ氏が作られたスライドを閲覧していますと、唐突にそのソリューションが示されました。以下のURLにありますので興味のある方はご覧ください。
「数学が自由すぎて地球がヤバい」という、およそ重力加速度とは関係なさそうなタイトルのスライドなのですが・・・。

もっちょ氏は「9.8」よりさらに細かい「9.80665」という値を用いて面倒な計算を実行して、やはり「計算が面倒」という結論を早々に出しておられます。

そして「地球の重力加速度を10にする」という方法を模索し始めます。天才的な着想ですね。

その考え方は次のようなものです。そもそも\(g\)は「万有引力の法則」というもので決まっています。地球が物体を引っ張る力ですね。この法則を用いると
\(g = GM/R^2\)
と表されます。
\(G\): 万有引力定数 (\(6.67\times 10^{-11}\)N・m\(^2\)/kg\(^2\))
\(M\): 地球の質量 (\(5.972\times 10^{24}\)kg)
\(R\): 地球の半径 (\(6371\)km)
ただし半径を式に代入する際はmに直しましょう(6371km→6371000m)。
ですので、\(g\)を9.8から10に増やすためには「質量\(M\)を少し増やせばよい」と思い当たります。\(R\)を変化させずに質量\(M\)を増やすことで\(g\)を9.8から10に増やすためには、
\(10 = GM_*/R^2\)
という式から\(M_*\)(増加後の質量)を求めると
\(M_* =6.095\times 10^{24}[\textrm{kg}]\)
を得ます。これが「重力加速度が10の地球の質量」ですから、ここからもともとの地球の質量を引いて
\(M_* – M = 1.23\times 10^{23}[\textrm{kg}]\)
を求めます。これだけの質量を地球に埋め込めば良い!ということですね。天才的な結論です。
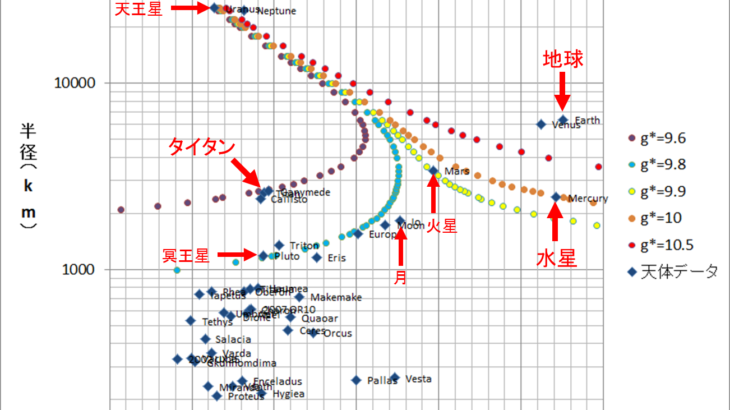
そんなちょうどいい質量の物体があるのか?と調べてみると、なんとあるんですね。土星の衛星「タイタン」です。地球とタイタンの大きさを比較するとだいたい5:2ですので、図に表すとこんな感じです。こんな大きなものを埋め込んで大丈夫なのか不安ですが・・・
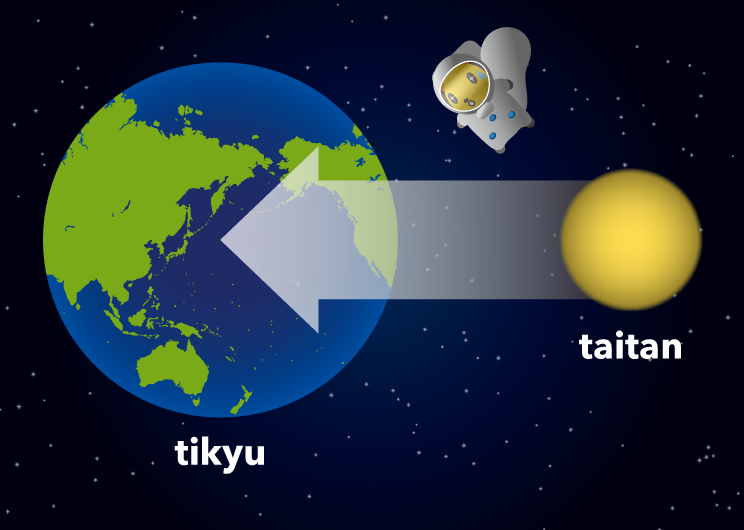
そしてもっちょ氏はタイタンを地球に埋め込みます。もっちょ氏のスライドから抜粋してgifアニメを作成させていただきました。

ゆ、有名なシミュレーション動画のパロディですね。ともかくこういった方法でタイタンの質量を地球に埋め込むと、\(g=10\)の地球ができあがるというわけです。
そしてもっちょ氏は「ここをこうするとどうなるんだろう」という創造性をいくらでも受け入れてくれるのが「数学」という学問なのだ、と結びます。今回ならば「半径を保ったまま重力加速度を10にするとどうなるんだろう」という創造性を受け入れてくれる、というわけですね。よくこんなこと思いつくなぁと大変楽しませていただきました。
タイタンが降り積もったら地球の半径が増えるのでは?
一服した後でよく考えてみると、ここまでの計算は「タイタンの質量が地球にプラスされるが、地球の半径は全く増えない」という前提で行っています。言い換えると、現在の地球の内部に十分なスキマがあって、そのスキマにタイタンの質量が入り込む余地があるという前提になっています。
でも普通に想像すると、衛星1個分の質量を格納できるようなスキマが地球の中にありますかね・・・?ないような気がするんですが・・・。むしろタイタンが降り積もったらその分、半径が増えてしまって計算が違ってくるのでは?と思いました。

というわけで、タイタンが降り積もった分だけ半径が増えると考えて計算し直してみましょう。まあたとえて言えば、タイタンを粉末にして地表にまんべんなく振りかけていくようなイメージですね。もしくは「タイタンという餅で地球というアンコをくるんだ大福餅」でしょうか。以下のようにして計算します。
地球の質量を\(M\)、半径を\(R\)とします。
タイタンの質量を\(M’\)、半径を\(R’\)、密度を\(\rho’\)とします。
地球にタイタンが降り積もったあとの「タイタン大福餅」の質量を\(M_*\)、半径を\(R_*\)とします。もちろん\(M_* = M+M’\)です。\(R_*\)はいくらになるでしょうか?

はい、\(R_*\)はこんな風に考えると求めることができます。
地球に降り積もったタイタンの部分(大福餅の餅の部分)に注目すると、この部分の質量は\(M’\)で密度が\(\rho’\)です。またこの部分の体積は\(\frac{4}{3}\pi R_*^3 – \frac{4}{3}\pi R^3\)です。以上のことから
\(M’ = \rho’\cdot \frac{4}{3}\pi (R_*^3 – R^3)\)
と表すことができます。この式の中で\(R_*\)以外の文字は全て分かっている値ですので、次のように\(R_*\)を求めることができます!
\(R_*^3 = \frac{3}{4\pi}\cdot \frac{M’}{\rho’} + R^3\)
ここで右辺の第一項の値は\(R’^3\)に等しいですね(\(M’ = \frac{4}{3}\pi R’^3\cdot \rho’\)のため)。ですので
\(R_*^3 = R’^3 + R^3\) … (1)
という風に簡単に書き表すことができます。何となく意外な結論ですね~。この右辺の値は分かっていますので、それらの数値を代入すれば\(R_*\)の値を求めることができる、すなわち「タイタン大福餅」の半径を求めることができるというわけです。
ということは「タイタン大福餅」の重力加速度も計算できる!
普通の地球の重力加速度は\(g = GM/R^2\)と書けますので、タイタン大福餅の重力加速度\(g_*\)は
\(g_* = \frac{G(M+M’)}{R_*^2}\) … (2)
と書き表すことができます。この右辺の値は全て分かりますので、こうしてタイタン大福餅の重力加速度も計算で求めることができるというわけです。
実際に数値を代入してみましょう。まずは半径\(R_*\)からです。先ほど式(1)で求めたように
\(R_*^3 = R’^3 + R^3\)
なので
\(R_* = (R’^3 + R^3)^{1/3}\)
ですが、ここで
地球の半径 \(R = 6371\)km
タイタンの半径 \(R’ = 2576\)km
を右辺に代入すると
タイタン大福餅の半径 \(R’ = 6508\)km
となります。最初の地球の半径よりほんのちょっと(137kmほど)増えただけですので、本当に薄皮の大福餅ですね。
そして式(2)に書いたように
\(g_* = \frac{G(M+M’)}{R_*^2}\)
ですが、ここで
地球の質量 \(M = 5.97\times 10^{24}\)kg
タイタンの質量 \(M’ = 1.34\times 10^{23}\)kg
を代入すると
\(g_* = 9.6\textrm{m/s}^2\)
と求めることができます!!!
なんと最初の重力加速度9.8よりも小さくなるんですね~。これは質量が大きくなった効果を半径が大きくなった効果が相殺してしまったからだと考えられるでしょう。
ここまでのまとめ、そして次なる展望
というわけで、当初の目的「重力加速度を10にする」を達成すべくタイタンを地球に降り積もらせてみたところ、確かにタイタンの質量分だけ地球は重くなるわけですが、同時に半径も大きくなってしまうため、重力加速度の式\(g=GM/R^2\)を用いると重力加速度はかえって小さくなってしまうということが分かりました。これはまことに残念です。
しかしここで引き下がる私ではございません。
式(1)と式(2)を組み合わせれば、どのような天体であっても地球に降り積もらせたときの重力加速度を求めることができます。ですので色々な天体のパラメータを代入してみて、重力加速度が10になるようなちょうどいい天体を探してみようではありませんか!次の記事ではそこをまとめてみたいと思っています。