1つ前の記事「重力加速度を10にするには①」では、地球の重力加速度の値が9.8m/s\(^2\)という半端な数字なのを嫌って、これが10になるように「土星の衛星タイタンを地球に埋め込み、地球の質量を大きくする」という策を検討しました。
この策が「アジマティクス」さんで発表された際には、タイタンを地球の中に埋め込んでも地球の半径は全く大きくならないという前提で計算がなされていました。しかしよく考えると地球の中にそんなスキマはないのでは?だからタイタンが地球に降り積もったら(これを「タイタン大福餅」と表現しました; 地球というアンコをタイタンという餅でくるんだイメージ)その分、地球の半径が大きくなるのでは?という私のアイデアをもとに計算してみると、残念ながら重力加速度は10にならず、9.6という値になってしまうのでした。
本記事はその続きで、「何とかして地球の重力加速度を10にしよう」という画策を続けます。
タイタンは密度が低すぎるのでは?
おさらいですが、重力加速度\(g\)を求める式は
\(g = GM/R^2\)
ですので、地球に何かが降り積もれば\(M\)が大きくなるので\(g\)は大きくなりそうですが、同時に\(R\)も大きくなるので、下手をすると逆に\(g\)は小さくなってしまうわけです。
調べてみるとタイタンは密度が1.9g/cm\(^3\)と地球(密度5.5g/cm\(^3\))に比べてかなり低密度なんですね。ですのでタイタンを地球に降り積もらせると、質量は確かに大きくなりますが、かなり半径も大きくなってしまうことが想像できます。これでは質量を大きくした効果が半径の増大によって打ち消されてしまうでしょう。
それならもっと高密度の天体を降り積もらせれば解決するはずです。高密度の天体と聞いてすぐに「中性子星」とか「白色矮星」とかを思いつく人はマニアですね。しかしそれらの天体は今度は地球に比べると質量が大きすぎて、重力加速度が10なんてもんじゃなくとんでもなく大きな値になってしまいます。今必要なのは、地球にちょっとトッピングすると重力加速度がちょっと増えるような、そういうビミョーな天体なのです。
密度高めの天体を調べると、地球の次は水星!
そもそも地球の密度5.5g/cm\(^3\)というのは大きい部類なのでしょうか、それとも小さい部類なのでしょうか?そういう疑問への強い味方が「絵でわかる宇宙地球科学」(寺田健太郎著)です。太陽系に関する最新の研究結果がこれでもかと盛り込まれています。
p.50にいい図がありました。太陽系内の天体の密度と半径のグラフです。
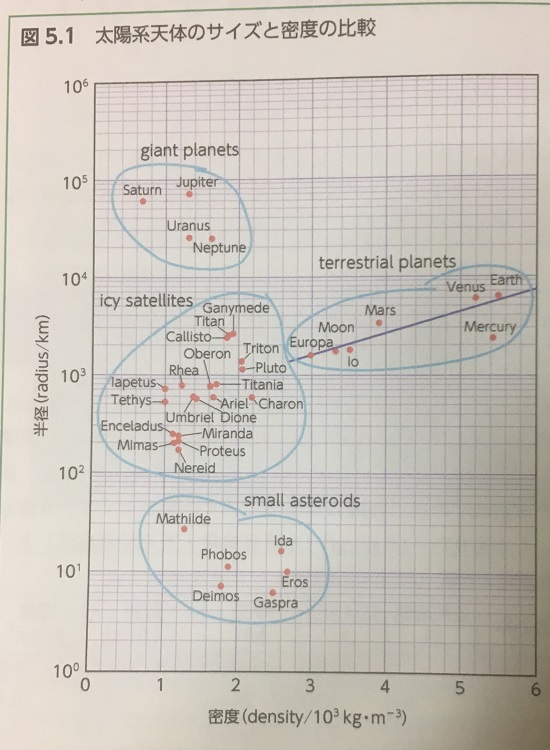
横軸が密度ですが、なんとこの図によると地球が一番高密度になっていますね。その次が水星、次が金星です。そこからちょっと間が空いて火星、イオ(木星の衛星)、月・・・と続いています。ですのでとりあえず水星とか金星あたりを調べてみたらいいんじゃないですかね。
では水星で調べてみましょう。1つ前の記事で「タイタン大福餅」を作ったように、今度は「水星大福餅」を作ります(地球というアンコを水星という餅でくるんだというイメージです)。地球の質量・半径をそれぞれ\(M\), \(R\)とし、水星の質量・半径をそれぞれ\(M’\), \(R’\)とすると、水星の質量が地球に降り積もったあとの半径\(R_*\)と重力加速度\(g_*\)は次の式で表されます。
\(R_*^3 = R’^3 + R^3\) … (1)
\(g_* = \frac{G(M+M’)}{R_*^2}\) … (2)
ここに数値を代入してみますと・・・
\(R_* = 6488\textrm{km}\)
\(g_* = 10.0\mathrm{m/s}^2\)
となります。おやっ!?!?!?いきなり\(g_*=10\)という望みの答えが出てきましたよ?これはなんという偶然でしょうか。地球の重力加速度を10にするためには、地球に水星を降り積もらせればOK!ということになりました!!
念のため金星の値を代入してみると、
\(R_* = 7831\textrm{km}\)
\(g_* = 11.8\mathrm{m/s}^2\)
となります。半径が水星大福餅に比べるとだいぶ大きくなっていますが、それ以上に質量が大きくなる効果があったのでしょうね(水星と金星の質量は14倍近く違います)。ですので重力加速度は10を超えてしまいました。
面白いので他の惑星や月でも一通り調べておきました。
月→9.8
火星→9.9
木星→24.9
土星→10.6
天王星→9.4
海王星→11.6
冥王星→9.8
たまたま最初に調べた水星が大ホームランでしたね。他の天体は惜しいものもありますが、「10.0」までたたき出した水星には敵いませんね(計算上は9.992…のようになるみたいですが)。
他にも\(g_*=10\)になる天体はないのか?
これで目的は達成したのですが、せっかく「絵でわかる宇宙地球科学」から図を参照させてもらったので、この図の中にほかにちょうどいい天体がないのか調べてみましょう。
まず、今後の準備のために自前で天体のデータを調べてグラフを作りました。データは全てwikipediaの「List of Solar System objects by size」というところから取ってきました。このURLでは天体がサイズ順に並べられており、半径200km以上の天体については密度も載っています。ここから半径と密度を拝借しました。
このデータを、密度を横軸、半径を縦軸にしてグラフに示しました。天体名も横に掲載してありますが、重なって見苦しいのは致し方ありません。このグラフが先ほどの「絵で分かる宇宙地球科学」に載っている図と本質的には同じものです。載ってる天体は少し違いますが。
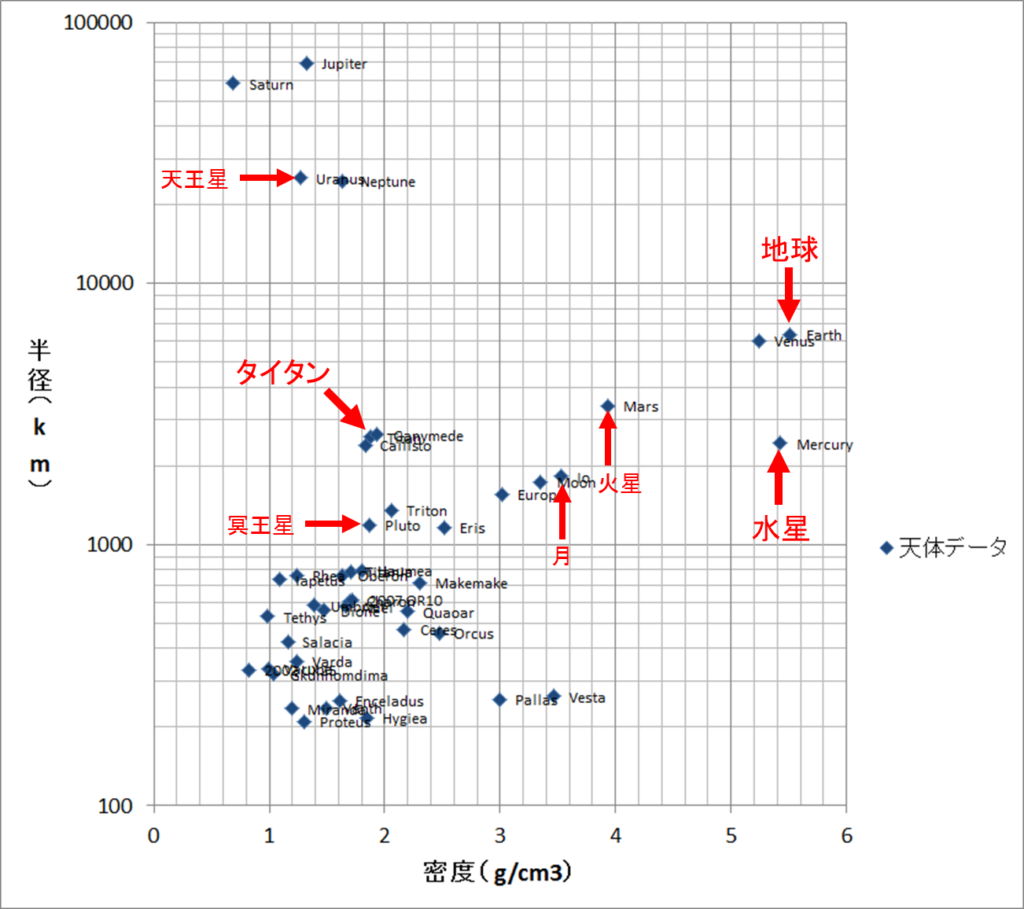
さて、このグラフ上に「地球上に降り積もらせたら地球の重力加速度が10になる(\(g_* = 10\)になる)ような天体」はどのくらいあるでしょうか。これって要するに「\(g_*\)が10になるような、密度\(\rho’\)と半径\(R’\)の関係式」を求めてグラフに表せばよいということですよね。式そのものは出そろっているのですから、計算すればできそうだと思いませんか?
で、やってみました。もしこの記事を高校生以上の人が読んでいるのなら、自分で計算してみるといいですよ。自信がつきますよ。では概略を説明します。用いた式は以下の3つです。
\(R_*^3 = R’^3 + R^3\) … (1)
\(g_* = \frac{G(M+M’)}{R_*^2}\) … (2)
\(M’ = \frac{4}{3}\pi R’^3 \rho’\) … (3)
\(R\): 地球の半径 (\(6371\)km)
\(R’\): 地球に降り積もる天体の半径
\(g_*\): 地球に天体が降り積もった後の地表での重力加速度
\(G\): 万有引力定数 (\(6.67\times 10^{-11}\)N・m\(^2\)/kg\(^2\))
\(M\): 地球の質量 (\(5.972\times 10^{24}\)kg)
\(M’\): 地球に降り積もる天体の質量
\(\rho’\): 地球に降り積もる天体の密度
目的のために邪魔なのは\(R_*\)と\(M’\)なので、この2文字を消すという意識で式変形を行います。具体的には(1)の\(R_*\)を(2)の分母に代入するのと、(3)の\(M’\)を(2)の分子に代入するのです。するとこんな式になります。
\(g_* = \frac{G}{(R’^3 + R^3)^{2/3}} \left( M + \frac{4}{3}\pi R’^3\cdot \rho’ \right)\)
これはグチャグチャな式に見えますが、\(\rho’\)と\(R’\)以外の文字は全て数値で表せますので、ほぼ目的は達成できています。ただ、これどうやってグラフに表すんですかね・・・。と思ったら、よく見たら\(\rho’\)は1次の項しかありません。ということは\(\rho’=…\)の形に変形すれば普通の関数として扱うことができますね。こんな感じです。
\(\rho’ = \left(\frac{g_*\cdot (R’^3 + R^3)^{2/3}}{G} – M\right)\cdot \frac{3}{4\pi R’^3}\)
大変な式に見えるかもしれませんが、右辺の\(R’\)以外は全て数値を代入すればいいので、いわゆる普通の関数です。というわけで先ほどの天体データに重ねてグラフの線を引いてみましょう。ただし右辺の\(g_*\)だけはこちらで好きな値を決めることができますので、9,6, 9.8, 9.9, 10.0, 10.5の5本を引いてみましょう。
結果がこちらです!!
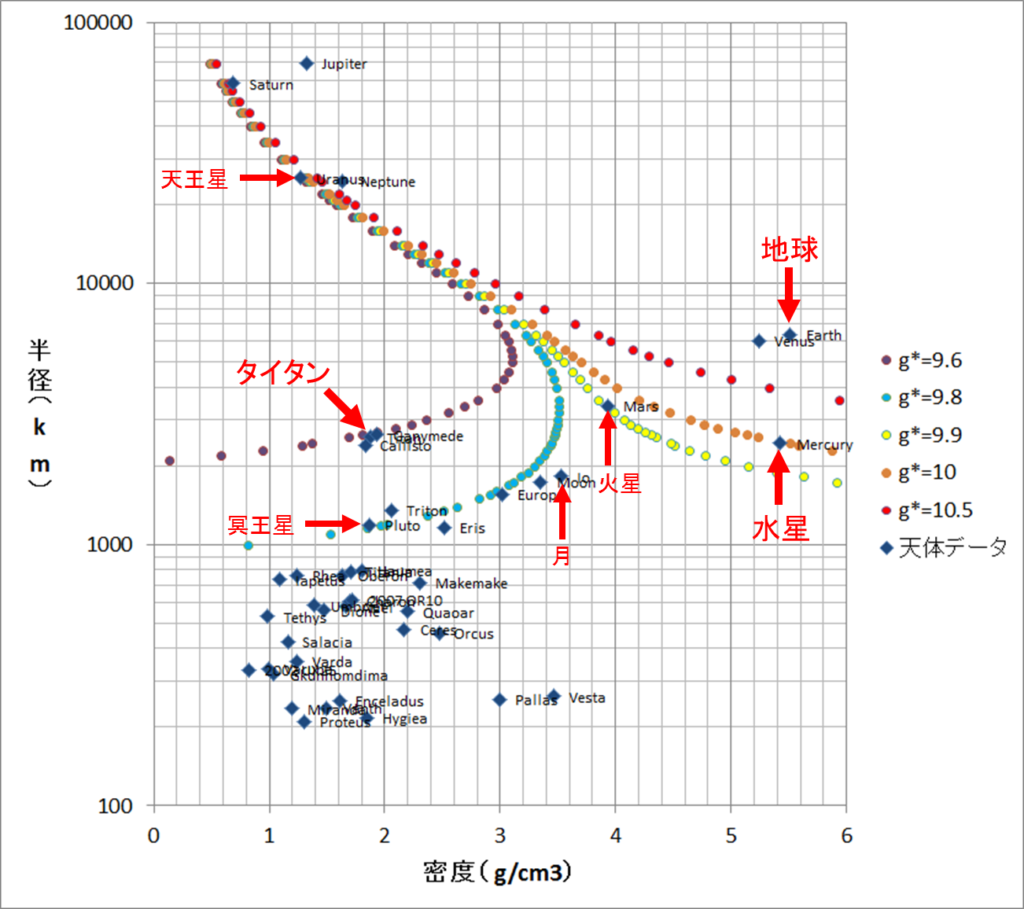
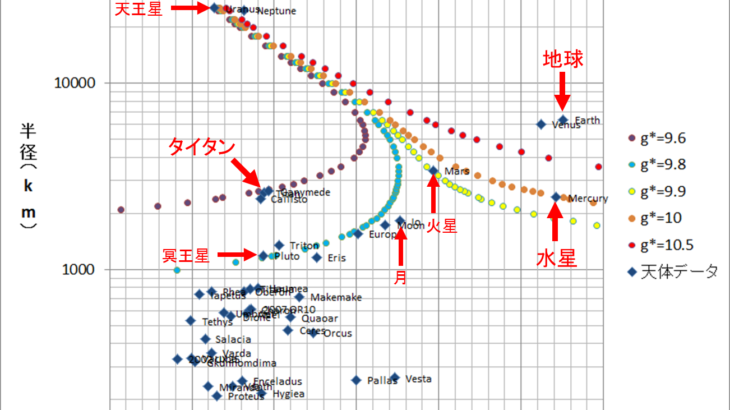
「引いてみましょう」と言ったものの、諸事情により線はナシで点だけになっています。さあゆっくり見てください。紫から赤までの5本のラインは「降り積もった後の\(g_*\)の値」に対応した計算結果です。
例えば一番左の紫のライン。このライン上にある天体が地球に降り積もると、重力加速度は\(g_* = 9.6\)になるというわけです。タイタン(Titan)がちょうどこのライン上にあります。
左から2番目の青のラインは\(g_*=9.8\)に対応しています。ちょうど冥王星がこのラインに載っていますが、冥王星は前の節の最後に計算してみましたね。確かに9.8になっていました。前の節の最後では月も9.8になる奴だったと思いますが、このグラフ上ではちょっと外れているように見えますね。調べてみると9.81のライン上に載っていますのでヨシとしましょう。
3番目の黄色のラインは\(g_*=9.9\)に対応していますが、火星がちょうどここに載っています。これまた前の節の最後の計算結果と一致しますね。
そしてお待ちかねのオレンジのライン!これが\(g_*=10\)に対応したラインです。この線上に見事に載っているのが水星です!また、このオレンジのラインに載っかる天体は非常に少ない(というか水星しかない)ということが分かります。左上の方で天王星も載っかっているように見えますが、あのあたりは多数のラインが混雑しており、少しでも横にずれると\(g_*\)の値が大きく変わってしまいます。実際、天王星は\(g_*=9.4\)ぐらいの天体です。
一番右の赤いラインは\(g_*=10.5\)ですが、ここに載っかる天体はないみたいですね。
このように見てみると、太陽系の天体はいろいろあるものの、地球に降り積もったときに重力加速度が10になる天体は非常に珍しく、恐らく水星以外にはない!ということが分かります。たまたま上では最初に目についた(密度が大きいということで試してみたのです)ので計算してみたのですが、他にはないんだということがここの計算で分かりました。
いや~スッキリしましたね。
\(g\)の近辺でラインが大きく動く
あとは蛇足かもしれませんが、先ほどの5本のラインって、上の方ではほぼ1本に収束しているのに対し、下の方では左と右に分かれていますよね。この左右の分かれ目は何で決まっているのでしょうか?9.8と9.9の間で左右が分かれているようですので、多分これは地球の重力加速度が境目になっているのでしょう。
今回計算に使った数値を用いると、地球の重力加速度\(g\)は
\(g = 9.81965\)
ぐらいです。\(g_*\)がこの値の前後を動くとグラフがどう変わるのかをプロットしてみました。
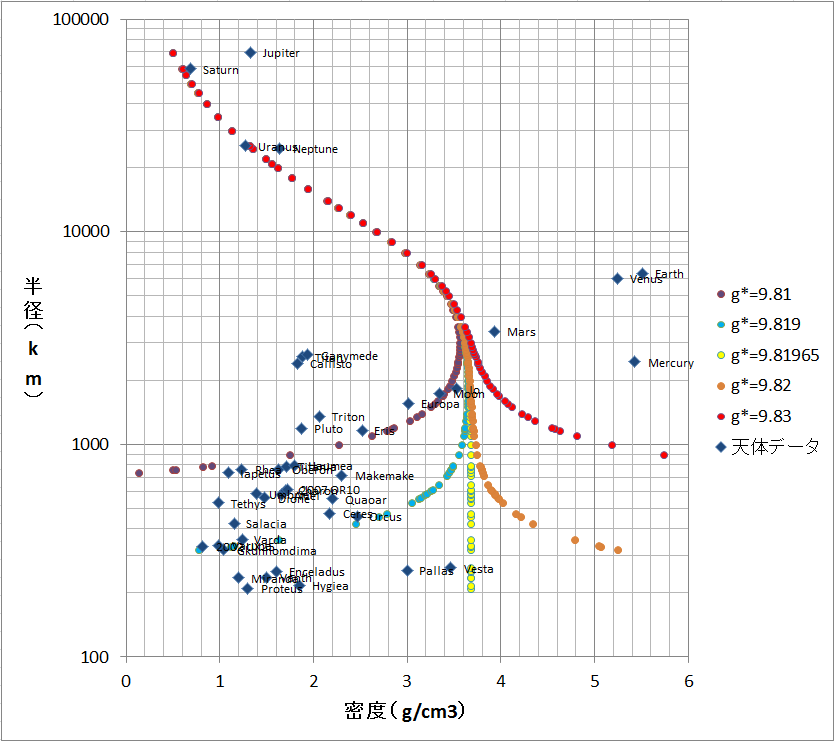
ご覧の通り、\(g_* = g\)となるラインは途中から真下に向かって伸びてますね。そして\(g_*\)がちょっとでも変わると左右にばらけるという様子がよく分かります。
真下に伸びた先は何だ?
まだ終わらないのかよ!と言われそうですが、さっきのグラフで黄色の点々が真下に伸びた行き先(\(g_* = g\)となるラインの行き先)の密度の値は何か意味があるのでしょうか?これまた計算して求めることができます。
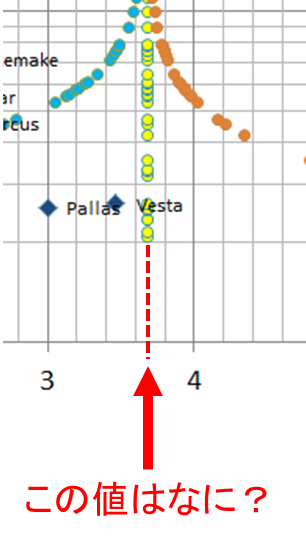
この値は、半径\(R’\)が小さくなった極限での密度\(\rho’\)の値ですので、上の方で用いた\(\rho’\)と\(R’\)の関係式から出発して、\(R’ \to 0\)の極限を考えていくと求めることができます。なお、この黄色の点々においては\(g_* = g\)となっていますので、以下の式中でも\(g_*\)の部分を\(g\)と書き換えてあります。
\(\rho’ = \left(\frac{g\cdot (R’^3 + R^3)^{2/3}}{G} – M\right)\cdot \frac{3}{4\pi R’^3}\) からスタート!
まずカッコの中の左の方にある\((R’^3 + R^3)^{2/3}\)から\(R^2\)を取り出して、\(R^2(1+(\frac{R’}{R})^3)^{2/3}\)と変形します。
\(\rho’ = \left(\frac{gR^2}{G}\cdot \left(1+ \left(\frac{R’}{R}\right)^3\right)^{2/3} – M\right)\cdot \frac{3}{4\pi R’^3}\)
ここで\(\frac{gR^2}{G} = M\)であることを利用すると、次のように少し簡単になります。
\(\rho’ = \frac{3M}{4\pi R’^3} \left\{ \left(1 + \left(\frac{R’}{R}\right)^3\right)^{2/3} -1\right\}\)
あとはここで\(R’ \to 0\)の極限を取ればいいですね。これはですね、\(x=R’/R\)とおいて微分の定義式だと考えるか、もしくは一般的に\(|a|\ll 1\)のとき成り立つ近似式
\((1+a)^n \approx 1+na\)
を用いるかすればOKです。後者の近似式を用いたと考えると次のような変形になります。
\(\rho’ \to \frac{3M}{4\pi R’^3} \left\{ 1 + \frac{2}{3}\cdot \left(\frac{R’}{R}\right)^3-1\right\}\)
\( = \frac{3M}{4\pi R’^3} \cdot \frac{2}{3}\cdot \frac{R’^3}{R^3}\)
\( = \frac{M}{2\pi R^3} (R’ \to 0) \)
このようになります。わりとスッキリしましたね。ところで地球の質量\(\rho\)は
\(\rho = \frac{M}{4\pi R^3/3} \)
ですので、これを用いると
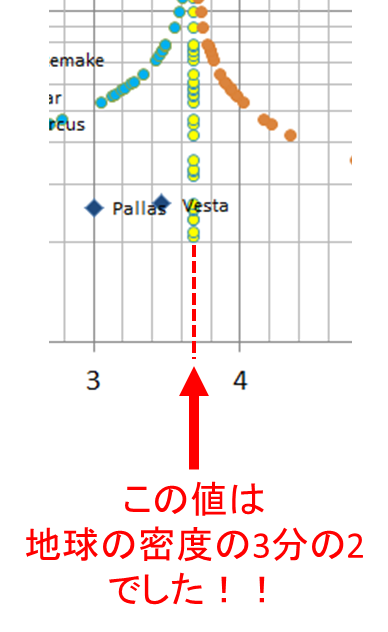
\(\rho’ \to \frac{2}{3}\rho (R’ \to 0)\)
となります。これが黄色の点々の行き着く先です。
つまり地球の3分の2の密度を持つ小さな天体が地球に降り積もっても、地球の重力加速度は変わらない(\(g_*=g\))ということです!!ただ、たまたまそのあたりのパラメータを持つ太陽系の天体は(調べた範囲のサイズだと)ないみたいですが・・・。
まとめ
いや~~まことに楽しかったですね。
もともとは鰺坂もっちょ氏の天才的な着想を面白がっていただけなのですが、ふと気になって計算してみただけでこんなに世界が広がりました。まさにもっちょ氏のおっしゃる
「ここをこうするとどうなるんだろう」という創造性をいくらでも受け入れてくれるのが「数学」という学問なのだ
ということを体感しました。数学というべきか物理というべきかよく分かりませんが、学問にそういう境目が必須であるわけではないので、必要なものを使って知りたかったことが分かった!ということで十分でしょう。
またこういうネタに巡り会いたいものです。